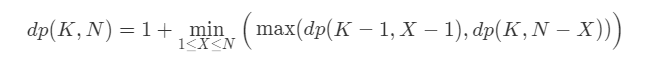5.24 Notes
5.18-5.24 Learning Notes
Leetcode
状态压缩+前缀和+哈希表
好题!
给你一个字符串 s ,请你返回满足以下条件的最长子字符串的长度:每个元音字母,即 ‘a’,’e’,’i’,’o’,’u’ ,在子字符串中都恰好出现了偶数次。
暴力
一开始我是暴力搜索的,从[0,len-1]出发,每次让左端点加一或者右端点减一,显然这样做会超时
class Solution
{
public:
const char vowel[5] = {'a', 'e', 'i', 'o', 'u'};
int count[6];
int ans;
void find(int l, int r, string &s)
{
if (l > r)
return;
bool flag = 1;
for (int i = 0; i < 5; i++)
{
if (count[i] % 2 != 0)
{
flag = 0;
break;
}
}
if (flag)
ans = max(ans, r - l + 1);
int tmp = 5;
for (int i = 0; i < 5; i++)
{
if (s[l] == vowel[i])
{
--count[i];
tmp = i;
break;
}
}
find(l + 1, r, s);
++count[tmp];
tmp = 5;
for (int i = 0; i < 5; i++)
{
if (s[r] == vowel[i])
{
--count[i];
tmp = i;
break;
}
}
find(l, r - 1, s);
++count[tmp];
}
int findTheLongestSubstring(string s)
{
for (auto each : s)
{
for (int i = 0; i < 5; i++)
{
if (each == vowel[i])
{
++count[i];
break;
}
}
}
find(0, s.size() - 1, s);
return ans;
}
};
优化
看了下提示,要用到bitmask和prefix sum,再结合题目“恰好出现了偶数次”的提示,不难想到要用异或来表示字符串的状态。
那就用每一位分别表示每一个元音字母出现的次数呗,1表示出现次数为奇数,0表示出现次数为偶数
前缀和是这样推想出来的:
aaee 00000
aee 00001
a 00001
sum["aee"]=sum["aaee"]^sum["a"]
sum[1,3]=sum[3]^sum[0]
类比sum[1,3]=sum[3]-sum[0],用前缀和求[1,3]的区间和
那现在我们要求:
sum[1,3]=0
即sum[3]^sum[0]=0
根据异或的交换律
sum[3]^0=sum[0]
等价于sum[3]=sum[0]
于是问题转化为:在所有[l,r]区间中,求满足sum[r]=sum[l-1]的最大区间。
后面我没有想到哈希表的方法,暴力应该过不了,所以偷偷看了评论
原理其实很简单:
- 如果当前的状态没有出现过,就把它加到哈希表里面
- 如果出现过,就计算区间长度,并维护
ans最大区间长度
状态只有1<<5=32个,所以可用数组来代替unordered_map
两个易错点:
- 哈希表里面记录的是
sum[l-1]第一次出现的位置,计算区间长度时需要注意len=r-hash_map[state]对应len=r-(l-1)=r-l+1 - 边界问题,如果最长字符串是从下标
0开始,即l=0,l-1=-1,所以初始化m[1...31]=-2,-2表示状态还未出现过,m[0]=-1,表示空字符串对应的状态为00000
这真的是一道middle题吗?建议大家认真消化知识点
class Solution {
public:
const char vowel[5] = {'a', 'e', 'i', 'o', 'u'};
int findTheLongestSubstring(string s)
{
int m[32];
int state=0;
int ans=0;
for (int i=0;i<32;i++)
m[i]=-2;
m[0]=-1;
for (int j=0;j<s.size();j++)
{
for (int i=0;i<5;i++)
{
if (s[j]==vowel[i])
{
state^=(1<<i);
break;
}
}
if (m[state]!=-2)
ans=max(ans,j-m[state]);
else
m[state]=j;
}
return ans;
}
};
CSAPP
Floating Point
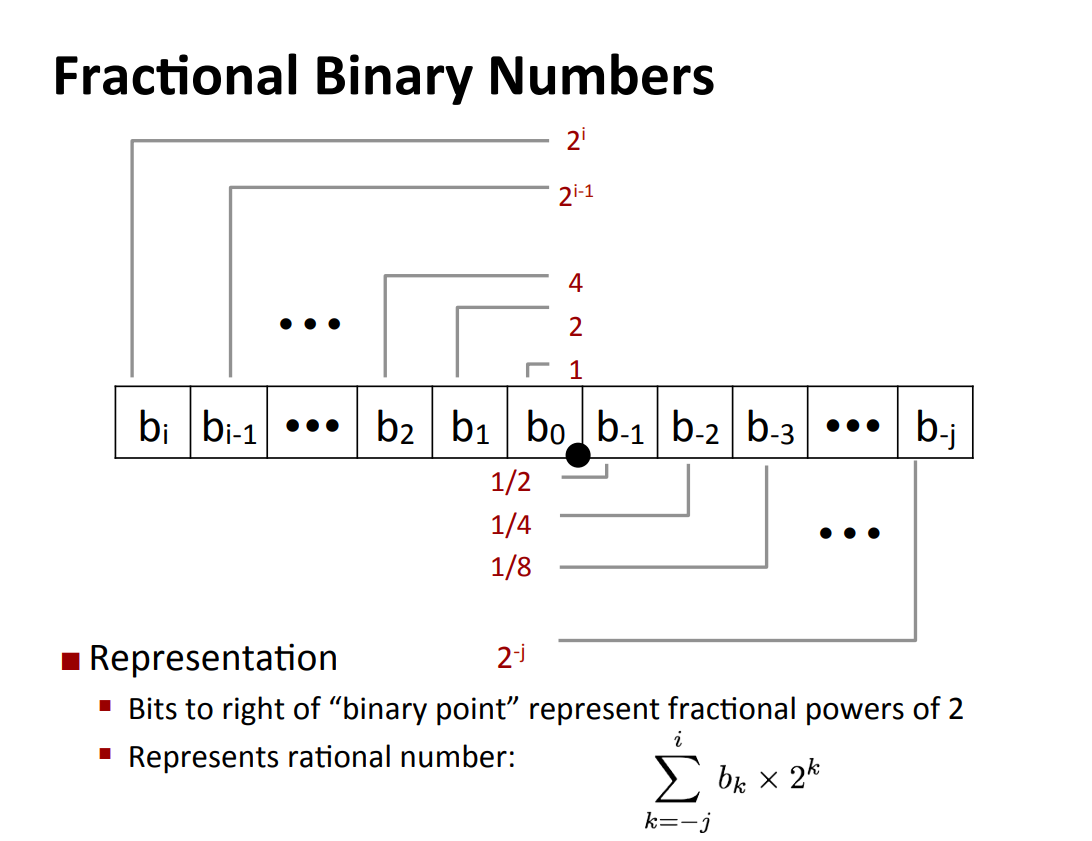
二进制浮点数表示:
$$ \sum^i_{k=-j}b_k*2^k $$
- $>>1=/2$
- $<<1=*2$
Limitation
- Can only exactly represent numbers of the form $x/2^k$
- 小数部分会占用整数部分的位数(在位数有限情况下)
IEEE Standard 754
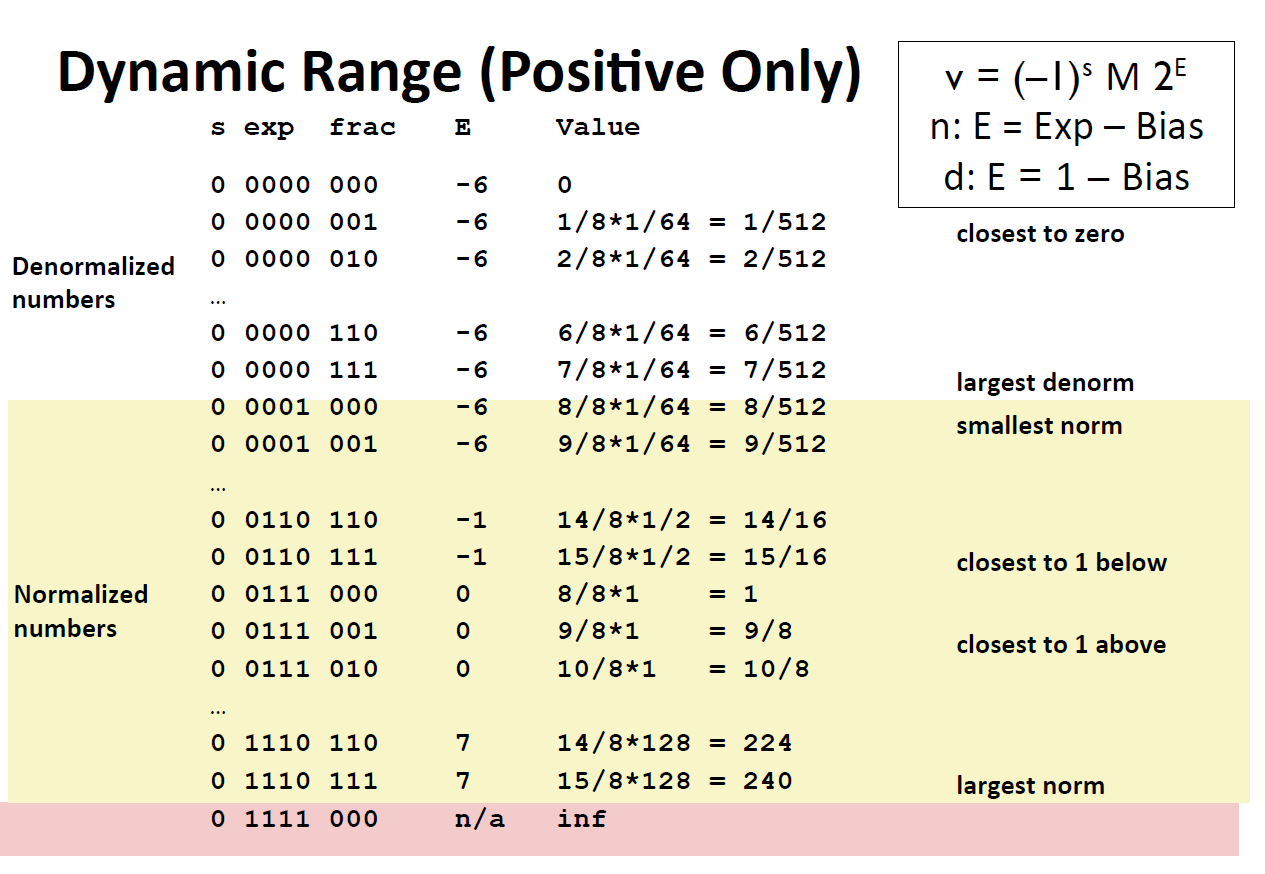
- Numerical Form:
$$ (-1)^sM2^E $$- $s$ is sign bit
- $M\in[1.0,2.0)$
- Exponent $E$
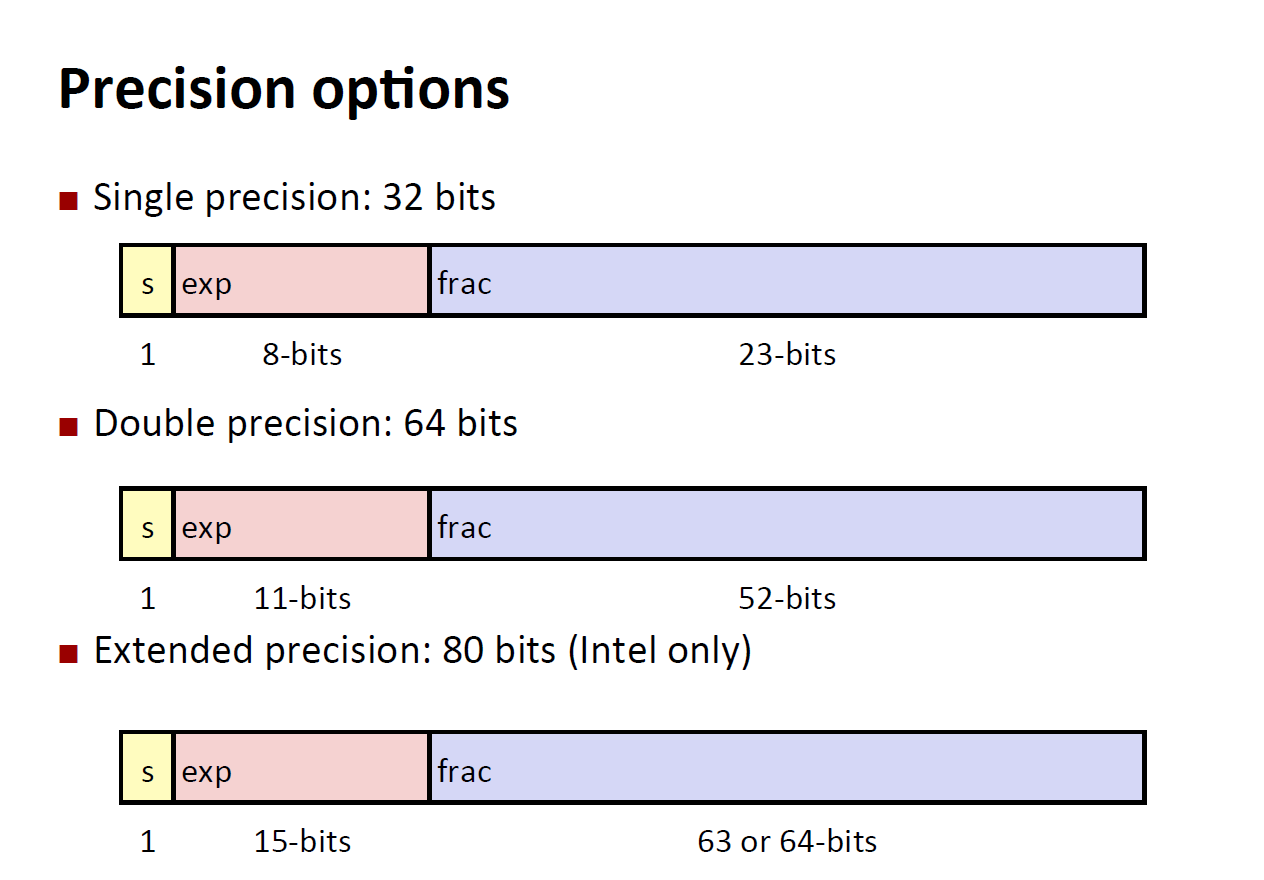
- Encoding
- $s|exp(E)|frac(M)$
- e.g.
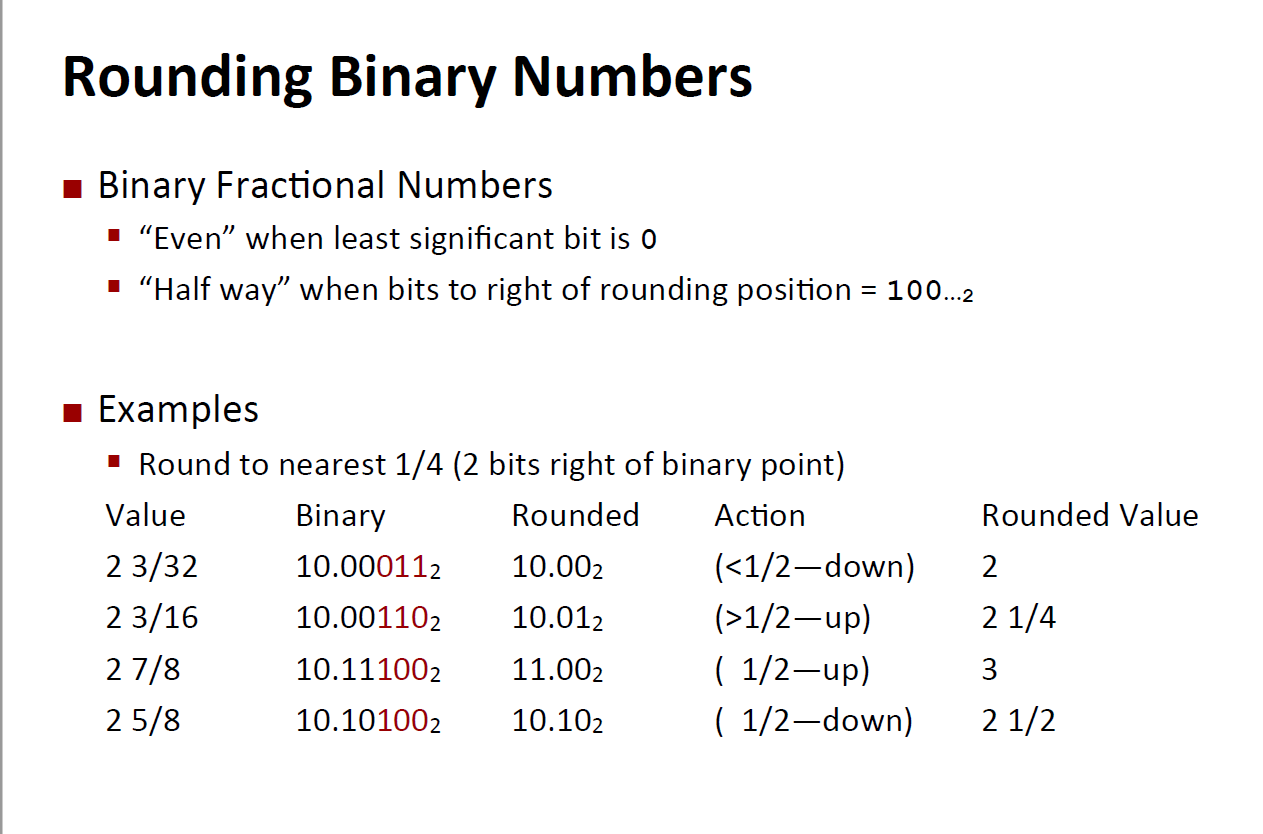
- Rounding
- Round to nearest even number: $1.4\approx1$, $1.5\approx2$
- Violates associativity
- Overflow and inexactness of rounding
- $(3.14+1e10)-1e10=10$, $3.14+(1e10-1e10)=3.14$
- Violates distributivity
Floating Point in C
- Conversions
- double/float->int
- Like rounding towards 0
- double的整数部分比int的多
- int->double exact
- int->float rounding
- double/float->int
Remember: Floating Point is not the Same as Real Number
Google Kick Start Round C
这场错过了,没有打实况。
2. Stable Wall
一道有点像俄罗斯方块的题目,已知俄罗斯方块游戏结束时的图案,求各个块落下的顺序
Apollo is playing a game involving polyominos. A polyomino is a shape made by joining together one or more squares edge to edge to form a single connected shape. The game involves combining N polyominos into a single rectangular shape without any holes. Each polyomino is labeled with a unique character from A to Z.
Apollo has finished the game and created a rectangular wall containing R rows and C columns. He took a picture and sent it to his friend Selene. Selene likes pictures of walls, but she likes them even more if they are stable walls. A wall is stable if it can be created by adding polyominos one at a time to the wall so that each polyomino is always supported. A polyomino is supported if each of its squares is either on the ground, or has another square below it.
Apollo would like to check if his wall is stable and if it is, prove that fact to Selene by telling her the order in which he added the polyominos.
我的想法
我的想法是模拟+dfs:
- 维护一个集合$S={当前可以放下的形状}$
- dfs遍历$S$并维护
supported数组(表示合法的放置位置)
写了一个多小时,才把样例过了…,然而一个测试集都没过
正解
Google的题还是挺需要转化的,这题其实不需要模拟。
每一个小块的落下要求:
- 它在底部
- 它的正下方已经有小块了
所以对于1~(n-1)的列,上下两个小块之间存在约束关系。我们可以用有向图来存储这种约束关系。每一对的约束关系都满足的条件下,能否找到一个合法的遍历这个图的序列。
显然,当图中存在环时不合法:
A<-->B
要放A就要先放B
要放B就要先放A
于是都放不了
用拓扑排序来判断有向图中有没有环,并得到拓扑序即为答案
3. Perfect Subarray
题意很简单,求一个数组中,子数组(数组中连续元素组成)的和为完全平方数的个数。
第一个测试集N=1000可以直接暴力判断,我学到了一个新函数modf
double res = sqrt(sum[i] - sum[j - 1]);
double f;
if (modf(res, &f) == 0.0)
++ans;
第二个测试集n=1e5肯定不能暴力了,怎么办呢?
那就看题解吧,反正想不出来了
题解确实很巧妙:
- 注意到每个数组元素$A_i\in[-100,100]$,用类似于计数排序的方法,哈希表
m[x]存储到当前元素为止,前缀和等于x的子数组个数 - 枚举的时候,第二层枚举可能的完全平方数,用逆向思维求$[1,i]$内以
A[i]结尾的,和为完全平方数的子数组个数$[1,i]=[1,k]+[k+1,i]$。我们不知道有多少个$sum[k+1,i]=完全平方数$,但是我们知道$[1,k]=sum[1,i]-完全平方数$的个数
int sum[100005];
void solve()
{
int n;
cin >> n;
ll ans = 0;
unordered_map<int, int> num_prefix_sum;
int minx = 0;
for (int i = 1; i <= n; i++)
{
int res;
cin >> res;
sum[i] = sum[i - 1] + res;
minx = min(minx, sum[i]);
}
num_prefix_sum[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 0;; j++)
{
int tmp = sum[i] - j * j;
if (tmp < minx)
break;
if (num_prefix_sum.count(tmp))
ans += num_prefix_sum[sum[i] - j * j];
}
num_prefix_sum[sum[i]]++;
}
cout << ans << endl;
}
Codeforces
来体验一下打CF的感觉
Round 643 div2
组合数学
https://blog.csdn.net/Fiveneves/article/details/106294338
Round 644 div3
Polycarp wants to buy exactly n shovels. The shop sells packages with shovels. The store has k types of packages: the package of the i-th type consists of exactly i shovels (1≤i≤k). The store has an infinite number of packages of each type.
Polycarp wants to choose one type of packages and then buy several (one or more) packages of this type. What is the smallest number of packages Polycarp will have to buy to get exactly n shovels?
For example, if n=8 and k=7, then Polycarp will buy 2 packages of 4 shovels.
Help Polycarp find the minimum number of packages that he needs to buy, given that he:
will buy exactly n shovels in total;
the sizes of all packages he will buy are all the same and the number of shovels in each package is an integer from 1 to k, inclusive.
题意还是很简单的:从$[1,k]$中找出最大的x,使$n%x==0$,$ans=n/x$
但是我卡了很久也没有做出来
错误思路
找一个数的因数嘛,我就想到用质数表了,$\sqrt{1e9}\approx31700$范围也不大,算法伪代码如下:
for prime in [2,sqrt(n)]:
if n%prime==0 and n/prime<=k:
return prime
枚举$n$的质因子,找到最小的满足条件的质因子就是答案了
但是这里其实有不少问题:
- 这个满足条件的质因子可能大于$\sqrt{n}$
- 答案不一定是一个质数
正确思路
for (int i = 1; i <= maxdiv; i++)
{
if (n % i == 0)
{
if (i <= k)
ans = min(ans, n / i);
if (n / i <= k)
ans = min(ans, i);
}
}
遍历$[1,\sqrt{n}]$,找$[1,\sqrt{n}]$的ans和$(\sqrt{n},n]$范围内的ans:
- 如果
i是ans,我们找的是最小的ans,同时需要满足每一份的大小n/i<=k - 如果
i是每一份的大小n/ans,i=n/ans<=k,份数ans=n/i
5.17 Notes
5.11-5.17 Learning Notes
CART
CSC1001 project
CART分类,预测app的Rating
实现CART过程中犯了不少错误
100%准确率
把Rating放到特征列里面,用测试集测试的时候还能偷偷用上测试集中Rating的数据,完美!
Gini Index计算
通俗来说,Gini Index是描述一堆数据中对目标列(Rating)的预测一致性
$$ GiniIndex(D,a)=\sum^V_{v=1}\frac{|D^V|}{|D|}Gini(D^v) $$
$$ Gini(D)=1-\sum^K_{k=1}(\frac{|C_k|}{|D|})^2 $$
where a is the selected feature, V is the number of splitting in datasetD, K is the number of labels. C_k is the size of the kth label in datasetD.
In our model, V=2 and K=2 because datasetD is split into 2 parts and there are only 2 labels which are Rating>4.5 and Rating<=4.5.
$$ Gini_index(D,a)=pGini(D^1)+(1-p)Gini(D^2) $$
$$ Gini(D)=1-p’^2-(1-p’)^2 $$
$$ p=\frac{|D^1|}{|D|} $$
$$ p’=\frac{|C^1|}{|D|} $$
华为软挑2020总结
我离决赛就差了一点实力哈哈,今年的辣鸡题目和命题组砖家已经给了我机会了
double精度问题
本质上是二进制与十进制转换过程中的误差
复赛B榜赛题中,明确金额的小数部分不超过两位,因此应该让金额*100,将其转换成整数
比赛回顾
上分全靠看大佬思路分享
初赛
- 每次搜索跳过比当前点小的点,这样做就不需要判重,之前我一直在想用hash判断重复的环…
- 离散化ID,sort+unique+unordered_map(虽然初赛数据只有5万个点有用)
- 6+1 (dfs正向6步+负向1步)
- 3邻域剪枝,标记dfs负向3步能到达的所有点
- fread+fwrite (第一次用)
- 向量改数组存边
vector<int> GUV[MAX_NODE]–>GUV[MAX_NODE][MAX_OUT_DEGREE]
复赛
比初赛多了金额约束
- 4+3 一直听说过4+3,但是知道看了https://zhuanlan.zhihu.com/p/136785097才会实现
- 拓扑排序删去入度/出度为0的点,虽然不知道对线上数据有没有效果
- 用ans3存长度为3的环,ans4存…..,
int *ans[5] = {ans3, ans4, ans5, ans6, ans7};存它们的头指针 - 部分函数参数改成全局变量
- 多线程部分是队友最后几天写的,我还不会…
为啥最后程序跑的还是这么慢呢?
前排大佬开源:
- https://github.com/CodeCraft2020/CodeCraft2020
- https://github.com/yoghurt-lee/HuaWeiCodeCraft2020
- https://github.com/WavenZ/CodeCraft2020
- https://github.com/cxq80803716/2020codecraft
原因猜想:
- dfs递归改迭代
- 多线程负载均衡
- 除法改乘法,不用double:
0.2<=nxtc/nowc<=3–>nowc<=5*nxtc && nxtc<=3*nowc - memcpy代替数组赋值
Resources
5.10 Notes
5.4-5.10 Learning Notes
Leetcode
跳跃游戏
第一题求能否到达终点,第二题求到达终点的最小步数
两题都可以用贪心做
I
- 如果某一个作为起跳点的格子可以跳跃的距离是 3,那么表示后面3 个格子都可以作为 起跳点。
- 可以对每一个能作为起跳点的格子都尝试跳一次,把能跳到最远的距离不断更新。
- 如果可以一直跳到最后,就成功了。
II
我的代码:
- 使用
cnt数组记录跳到某一个位置所需的最小步数
class Solution
{
public:
int jump(vector<int> &nums)
{
int r = 0;
int n = nums.size();
int cnt[n];
memset(cnt, -1, sizeof(cnt));
cnt[0] = 0;
for (int i = 0; i < nums.size(); i++)
{
if (i + nums[i] <= r)
continue;
for (int j = r + 1; j < n && i + nums[i] >= j; j++)
cnt[j] = cnt[i] + 1;
r = i + nums[i];
if (r >= n)
break;
}
return cnt[n - 1];
}
};
精简后的代码(题解):
class Solution
{
public:
int jump(vector<int> &nums)
{
int r = 0;
int n = nums.size();
int step = 0;
int end = 0;
for (int i = 0; i < nums.size() - 1; i++)
{
r = max(r, i + nums[i]);
if (i == end)
{
end = r;
++step;
}
}
return step;
}
};
最低票价
初始思路:dp[i]表示完成前i个旅行计划所需要的最低消费
$dp[i]=\min{f[j]+costs[k]}$, $k=0,1,2$ ,$days[j]+t[k]>=days[i]$
$t[3]={1,7,30}$
这样定义dp方程的话是有后效性的。因为第i个旅行计划之前的消费都是确定的,有点类似贪心,没有考虑到当前还剩多少天的通行证。
正解:dp[i]表示前i天所需要的最低消费
- 如果当天不在计划内$dp[i]=dp[i-1]$
- 如果在计划内$dp[i]=\min{dp[i-1]+costs[0],dp[i-7]+costs[1],dp[i-30]+costs[2]}$
class Solution {
public:
const int inf=1<<30;
int mincostTickets(vector<int>& days, vector<int>& costs) {
int ticket[3]={1,7,30};
int n=days.size();
vector<int> dp(days[n-1]+1,0);
for (int i=0;i<n;i++)
dp[days[i]]=-1;
for (int i=1;i<=days[n-1];i++)
{
if (dp[i]==0)
dp[i]=dp[i-1];
else
{
dp[i]=min({dp[max(i-1,0)]+costs[0],dp[max(i-7,0)]+costs[1],dp[max(i-30,0)]+costs[2]});
}
}
return dp[days[n-1]];
}
};
5.3 Notes
4.20-5.3 Learning Notes
Huawei Sofeware Competition
First Round
成功水进复赛
思路:
- 三邻域剪枝
- 6+1
- 向量改数组
感谢:
- https://zhuanlan.zhihu.com/p/125764650
- https://blog.csdn.net/zhangruijerry/article/details/105268377
- https://github.com/byl0561/HWcode2020-TestData
code
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <array>
#include <chrono>
#include <cmath>
using namespace std;
auto time_start = chrono::steady_clock::now();
// #define LINUXOUTPUT
#define OUTPUT
#define TEST
string input_path = "/data/test_data.txt";
string output_path = "/projects/student/result.txt";
#ifdef TEST
string test_scale = "1004812";
string test_input_path_s = "./data/" + test_scale + "/test_data.txt";
string test_output_path_s = test_input_path_s.substr(0, test_input_path_s.rfind('/')) + "/output.txt";
#endif
const int INF = 280005;
typedef long long ll;
int GUV[INF][51];
int GVU[INF][51];
bool visited[INF];
int flag[INF];
typedef array<int, 8> ans_t;
int ans_size;
ans_t ans[4000005];
int u_max;
namespace IO
{
const int MAXSIZE = 1 << 20;
char buf[MAXSIZE], *p1, *p2;
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin), p1 == p2) ? EOF : *p1++)
inline int rd()
{
int x = 0;
int16_t c = gc();
while (!isdigit(c))
{
if (c == EOF)
return c;
c = gc();
}
while (isdigit(c))
x = x * 10 + (c ^ 48), c = gc();
return x;
}
inline void rd_to_line_end()
{
int16_t c = gc();
while (c != '\n')
c = gc();
}
char pbuf[MAXSIZE], *pp = pbuf;
inline void push(const char &c)
{
if (pp - pbuf == MAXSIZE)
fwrite(pbuf, 1, MAXSIZE, stdout), pp = pbuf;
*pp++ = c;
}
inline void write(int x)
{
static int sta[35];
int top = 0;
do
{
sta[top++] = x % 10, x /= 10;
} while (x);
while (top)
push(sta[--top] + '0');
}
} // namespace IO
inline void read_data()
{
freopen(test_input_path_s.c_str(), "r", stdin);
int u, v;
int ch;
register int i;
while (1)
{
u = IO::rd();
if (u == EOF)
break;
v = IO::rd();
IO::rd_to_line_end();
GUV[u][++GUV[u][0]] = v;
GVU[v][++GVU[v][0]] = u;
u_max = max(u_max, u);
}
#ifdef TEST
auto input_time_end = chrono::steady_clock::now();
auto input_time_diff = input_time_end - time_start;
cout << "prehandle cost: " << chrono::duration<double, milli>(input_time_diff).count() / 1000 << "s" << endl;
#endif
}
inline bool cmp(ans_t &x, ans_t &y)
{
int now = 0;
while (x[now] == y[now])
++now;
return x[now] < y[now];
}
void flag_reverse_dfs(int u, int depth, int target)
{
register int i;
int v;
for (i = 1; i <= GVU[u][0]; i++)
{
v = GVU[u][i];
if (!visited[v] && v > target)
{
visited[v] = 1;
flag[v] = target;
if (depth <= 2)
flag_reverse_dfs(v, depth + 1, target);
visited[v] = 0;
}
}
}
void dfs(int u, int depth, ans_t &path, int target)
{
register int i;
int v;
for (i = 1; i <= GUV[u][0]; i++)
{
v = GUV[u][i];
if (v <= target)
continue;
if (flag[v] == -target && visited[v] == 0)
{
if (depth >= 2)
{
path[0] = depth + 1;
path[depth + 1] = v;
ans[++ans_size] = path;
}
}
if (flag[v] != target && flag[v] != -target && depth >= 4)
continue;
if (!visited[v] && depth <= 5)
{
visited[v] = 1;
path[depth + 1] = v;
dfs(v, depth + 1, path, target);
visited[v] = 0;
}
}
}
inline void work()
{
ans_t path;
register int i, j;
int target;
for (i = 1; i <= u_max; i++)
{
if (GUV[i][0] == 0)
continue;
flag_reverse_dfs(i, 1, i);
for (j = 1; j <= GVU[i][0]; j++)
flag[GVU[i][j]] = -i;
path[1] = i;
dfs(i, 1, path, i);
}
}
inline void output_data()
{
register int i, j;
freopen(test_output_path_s.c_str(), "w", stdout);
sort(ans + 1, ans + ans_size + 1, cmp);
#ifdef TEST
auto output_time_start = chrono::steady_clock::now();
#endif
printf("%d\n", ans_size);
for (i = 1; i <= ans_size; i++)
{
for (j = 1; j < ans[i][0]; j++)
{
IO::write(ans[i][j]);
IO::push(',');
}
IO::write(ans[i][ans[i][0]]);
IO::push('\n');
}
fwrite(IO::pbuf, 1, IO::pp - IO::pbuf, stdout);
#ifdef LINUXOUTPUT
freopen("/dev/tty", "w", stdout);
#else
freopen("CON", "w", stdout);
#endif
#ifdef TEST
auto output_time_end = chrono::steady_clock::now();
auto output_time_diff = output_time_end - output_time_start;
cout << "output cost: " << chrono::duration<double, milli>(output_time_diff).count() / 1000 << "s" << endl;
#endif
return;
}
int main()
{
read_data();
work();
output_data();
#ifdef TEST
auto time_end = chrono::steady_clock::now();
auto diff = time_end - time_start;
#ifdef LINUXOUTPUT
freopen("/dev/tty", "w", stdout);
#else
freopen("CON", "w", stdout);
#endif
printf("ans size is %d\n", ans_size);
cout << "The program's speed: " << chrono::duration<double, milli>(diff).count() / 1000 << "s" << endl;
#endif
fclose(stdin);
fclose(stdout);
return 0;
}
总结
- 多看群信息
- 多上网找别人的思路
- 钻规则漏洞:开小号/探测数据(误)
面向数据编程
Level 1: 计分数据只有一组
以下设 answer 表示找到的环数。
加入如下代码:
assert(answer > 2500000);提交后返回 Runtime Error。断定:线上存在环数不大于 2500000 的数据。
加入如下代码:
if (answer <= 2500000) { sleep(100); }提交后分数不变。断定:环数不大于 2500000 的数据不计分。
加入如下代码:
if (answer > 2500000) { if (rand() & 1) sleep(100); }多次提交,每次分数都不变。断定:对于一组数据,运行了多次,取最快的一次作为分数。
加入如下代码:
if (answer > 2500000) { sleep((answer - 2500000) / 1000); }提交后返回 414。断定:某一组数据的答案除以 1000 为 2914。
加入如下代码:
if (answer / 1000 == 2914) { sleep(answer % 1000); }提交后返回 186。断定:上述数据的答案为 2914186。
加入如下代码:
if (answer > 2500000) { assert(answer == 2914186); }提交后正常返回。断定:线上计分的数据只有一组,且答案为 2914186。
Level 2: 计分数据分布极不规律
以下设 src[i] 表示以 i 为起点的环数。
加入如下代码:
if (answer == 2914186) { int max_src = 0; for (int i = 0; i <= n; i++) { max_src = max(max_src, src[i]); } sleep(max_src * 100 / answer); }提交后返回 26。表明存在一个点,以其为起点的环不少于 2914186 * 0.26 = 757688 个。
加入如下代码:
if (answer == 2914186) { vector<int> vec; for (int i = 0; i <= n; i++) { if (src[i]) vec.push_back(src[i]); } sort(vec.begin(), vec.end()); sleep(vec[(int)vec.size() - 2] * 100 / answer); }提交后返回 13。表明存在另外一个点,以其为起点的环不少于 2914186 * 0.13 = 378844 个。
使用类似的方法,可以得出还有另外一个点,以其为起点的环也不少于 378844 个。
Level 3: 根据数据特点进行优化
使用 Level 1 中介绍的方法,可以得出如下信息:线上的点数为 20W,其中出现在答案里的点数为 4.2W,出现在答案里的点的最大值为 49999。所以优化策略如下:读入时,直接忽略 >= 5W 的节点。
使用 Level 2 中介绍的方法,得出:以 6000, 10000, 10001, 25123 这四个点为起点的环非常多,在给线程分配任务时可以特殊处理。
加入如下代码:
if (answer == 2914186) { int max_src_i = 0; for (int i = 0; i <= n; i++) { if (src[i]) max_src_i = i; } sleep(max_src_i / 1000); }提交后返回 43。表明不存在满足“环中的最小值大于 44000”的环,所以枚举起点时只需要枚举到 44000。
Level 4: 猜测数据生成规则
下述 K12, K13 分别表示 12 个点、13 个点的有向完全图。容易知道,对于 K_n,其中长度为 m(3<=m<=n) 的环数为 C(n,m) * (m-1)!。
使用 Level 2 中介绍的方法,得出:以 10000 为起点的环大约为 757688 个;以 6000, 10001 为起点的环大约为 378844 个。
观察到:设 1, 2, 3, …, 13 这 13 个点组成一个 K13,那么以 1 为起点的长度介于三和七之间的环的个数为 773652 个,这个数字和 757688 十分接近。同时可以发现,以 2 为起点的长度介于三和七之间的环的个数为 397100,这个数字和 378844 十分接近。由此猜测:10000, 10001, …, 10012 这 13 个点组成了一个 K13。经验证果然如此!
使用相同的做法可以发现,6000, 6001, …, 6011 这 12 个点组成了一个 K12,25123, 25124, …, 25134 这 12 个点也组成了一个 K12。
结合 Level 3 中的结论 “答案中最大的点为 49999”,猜测:大于等于 50000 的点连成一个 DAG 森林,没有环出现。
对于 K13,其中长度介于三和七之间的环的个数为 1477190。对于 K12,其中长度介于三和七之间的环的个数为 703538。所以仅仅这三个团的环数已经有 2884266 个,而总环数只有 2914186 个,也就是说除了这三个团,只有 29920 个环。这些环是很容易生成的,推测是使用了某种随机算法。
综上:10000, 10001, …, 10012 这 13 个点组成了一个 K13,6000, 6001, …, 6011 这 12 个点组成了一个 K12,25123, 25124, …, 25134 这 12 个点也组成了一个 K12。其余的小于 50000 的点随机连边。大于等于 50000 的点连成 DAG 森林。
Leetcode滑动窗口+map/multiset
只有滑动窗口的代码
思路:
若maxn-minx>limit,将滑动窗口左端点右移
否则扩大窗口,将右端点右移
答案就是最大的滑动窗口大小
class Solution
{
public:
int longestSubarray(vector<int> &nums, int limit)
{
int ans = 1;
int len = 0;
int minx = 1 << 30;
int maxn = 0;
for (int j = 0; j < nums.size(); j++)
{
len = 1;
minx = nums[j];
maxn = nums[j];
for (int i = j + 1; i < nums.size(); i++)
{
maxn = max(maxn, nums[i]);
minx = min(minx, nums[i]);
if (maxn - minx > limit)
{
ans = max(len, ans);
break;
}
else
{
++len;
}
}
ans = max(len, ans);
}
return ans;
}
};
+map/multiset
上面的程序在每次滑动窗口右移的时候,都要重新计算滑动窗口中的最大值和最小值。
所以可以用map(红黑树)来维护滑动窗口中的最大值和最小值,右移的时候就删掉窗口左端点的值,扩大窗口的时候就插入右端点的值
class Solution
{
public:
int longestSubarray(vector<int> &nums, int limit)
{
map<int,int> m;
int ans = 1;
int j=0;
for (int i=0;i<nums.size();i++)
{
// insert
++m[nums[i]];
// maxn-minx>limit
if (m.rbegin()->first-m.begin()->first>limit)
{
// window right shift
--m[nums[j]];
if (m[nums[j]]==0)
m.erase(nums[j]);
++j;
}
else
{
// calculate window's size
ans=max(ans,i-j+1);
}
}
return ans;
}
};
4.19 Notes
4.13-4.19 Learning Notes
Leetcode
一道较难的dp题:鸡蛋掉落
dp
注意dp数组的初始化:
- 0个蛋
- 1个蛋
- 0层楼
- 1层楼
// init
for (int k = 1; k <= K; k++)
for (int n = 1; n <= N; n++)
dp[k][n] = INF;
for (int k = 1; k <= K; k++)
{
dp[k][0] = 0;
dp[k][1] = 1;
}
for (int n = 1; n <= N; n++)
{
dp[0][n] = 0;
dp[1][n] = n;
}
for (int k = 2; k <= K; k++)
{
for (int n = 2; n <= N; n++)
{
for (int x = 1; x <= n; x++)
{
dp[k][n] = min(dp[k][n], max(dp[k - 1][x - 1], dp[k][n - x]) + 1);
}
}
}
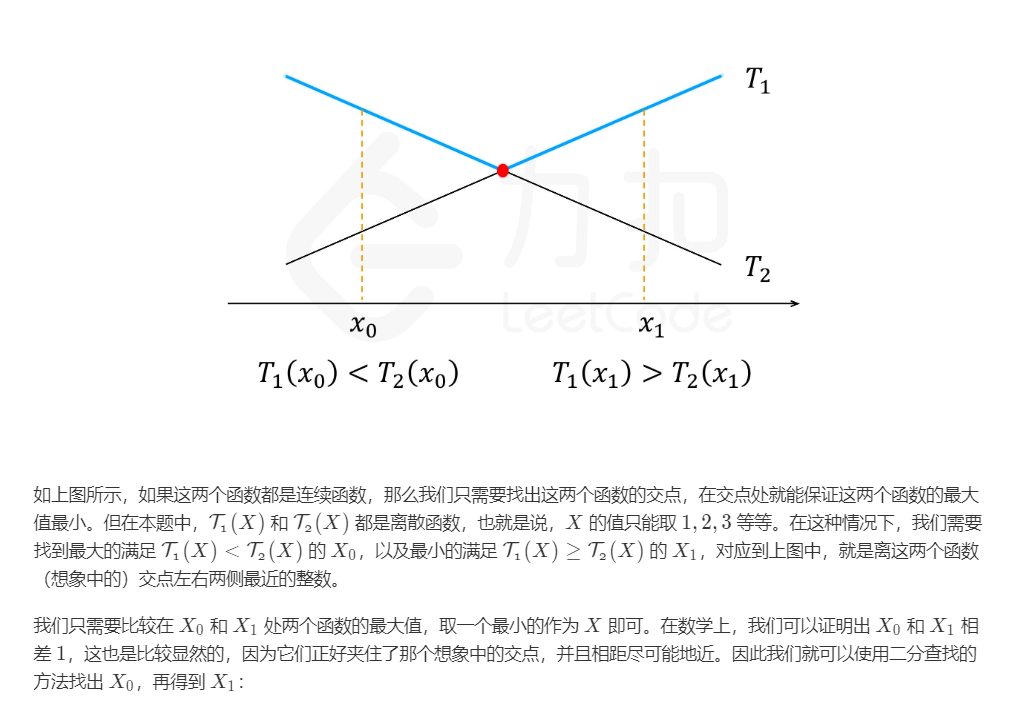
dp+二分搜索
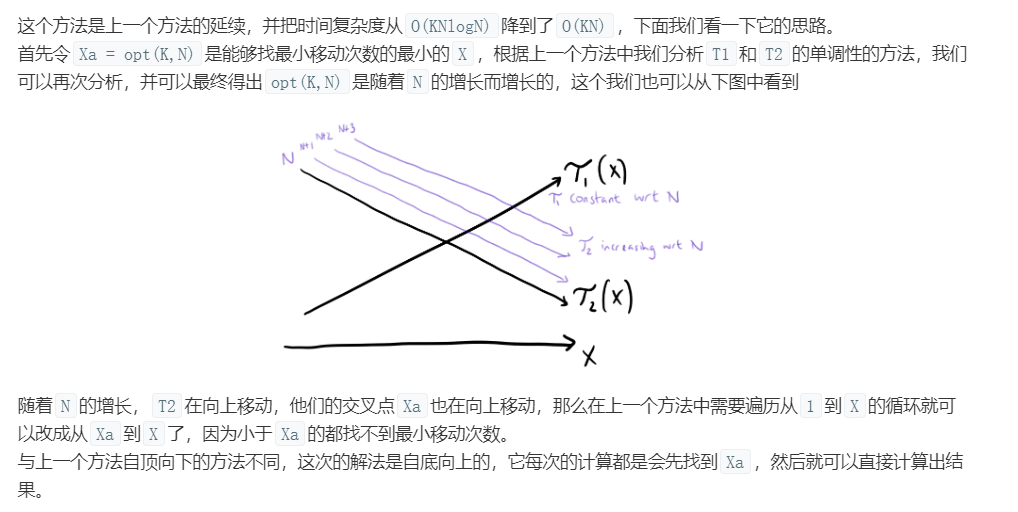
二分搜索出$X_0$后,$X_1=X_0+1$,最后我们要取$min{max(T_1(X_0),T_2(X_0)),max(T_1(X_1),T_2(X_1))}$
显然$T_1(X_0)<=T_2(X_0)$,$T_1(X_1)>T_2(X_1)$
所以最后取$min(T_2(X_0),T_1(X_1))$
因此我们可以把第三层的循环改成二分搜索求山谷值valley,二分搜索求山谷值是一个难点:
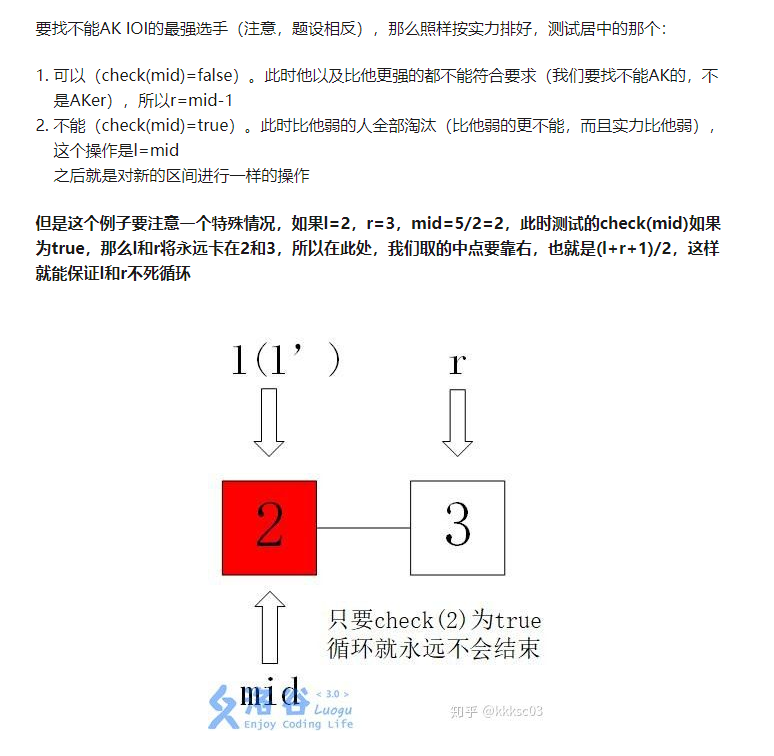
浅谈二分的边界问题
这里的中点要取靠右的中点mid=(l+r+1)/2
for (int k = 2; k <= K; k++)
{
for (int n = 2; n <= N; n++)
{
int le = 1, ri = n;
while (le < ri)
{
// 取靠右的中点
int mid = (le + ri + 1) / 2;
// 表示能AK
// 取等时也算不能AK
if (dp[k - 1][mid - 1] > dp[k][n - mid])
ri = mid - 1;
else
le = mid;
}
dp[k][n] = min(dp[k][n - le], dp[k - 1][le]) + 1;
}
}
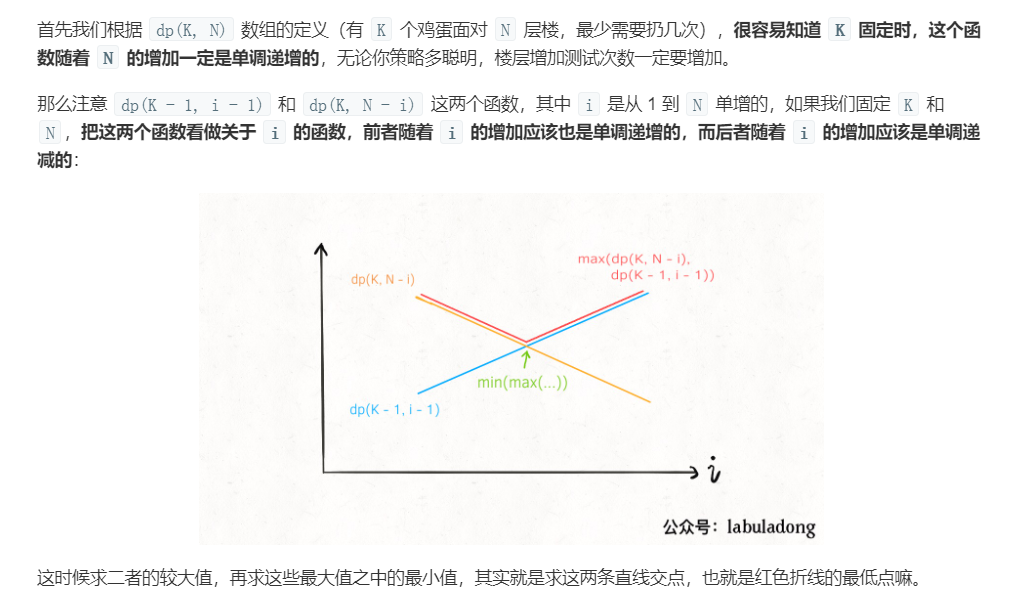
dp+决策单调性
k一定,n增大,$T_2(x)=dp(k,n-x)$向上移动,$T_1(x)=dp(k-1,x-1)$不动,每次只需要从上一个n得到的x出发即可。
for (int k = 2; k <= K; k++)
{
int x = 1;
for (int n = 2; n <= N; n++)
{
while (x < n && dp[k][n - x] > dp[k - 1][x - 1])
{
++x;
}
dp[k][n] = dp[k - 1][x - 1] + 1;
}
}
剧情触发时间
在战略游戏中,玩家往往需要发展自己的势力来触发各种新的剧情。一个势力的主要属性有三种,分别是文明等级(C),资源储备(R)以及人口数量(H)。在游戏开始时(第 0 天),三种属性的值均为 0。
随着游戏进程的进行,每一天玩家的三种属性都会对应增加,我们用一个二维数组 increase 来表示每天的增加情况。这个二维数组的每个元素是一个长度为 3 的一维数组,例如 [[1,2,1],[3,4,2]] 表示第一天三种属性分别增加 1,2,1 而第二天分别增加 3,4,2。
所有剧情的触发条件也用一个二维数组 requirements 表示。这个二维数组的每个元素是一个长度为 3 的一维数组,对于某个剧情的触发条件 c[i], r[i], h[i],如果当前 C >= c[i] 且 R >= r[i] 且 H >= h[i] ,则剧情会被触发。
根据所给信息,请计算每个剧情的触发时间,并以一个数组返回。如果某个剧情不会被触发,则该剧情对应的触发时间为 -1 。
当时的想法
当时比赛做题的时候,首先想到暴力做法:对于每一天的c,r,h,暴力检查是否满足某个条件
然后想优化暴力,如何快速的找到可能满足的条件
要不就用三个优先队列(最小堆)来维护条件吧,每次取他们的头部看看是否满足条件
写完发现样例过不去,问题就在于当前满足的条件不一定在三个优先队列的头部。用极端点的例子来解释:
requirements=[[1,1e10,1e10],[1e10,1,1e10],[1e10,1e10,1],[2,2,2]]
显然前三个条件是很难满足的,容易满足的第四个条件又不在队列头部
正解
我们应该去找,对于每一个条件的c,r,h,找到它们分别需要的最小天数,该条件所需的天数就是三个属性的所需最小天数的最大值
从另一个角度,即遍历每一个条件,c,r,h三个属性是相对独立的,它们需要的最小天数可以分别算出来,然后再取最大值
具体算法:
算出increase的前缀和,分别找到三个属性恰好满足条件的天数,取它们的最大值,就是当前剧情的触发时间
Google Code Jam Round 1A 2020
Pattern Matching
Problem
Many terminals use asterisks * to signify “any string”, including the empty string. For example, when listing files matching BASH*, a terminal may list BASH, BASHER and BASHFUL. For FUL, it may list BEAUTIFUL, AWFUL and BASHFUL. When listing BL, BASHFUL, BEAUTIFUL and BULL may be listed.
In this problem, formally, a pattern is a string consisting of only uppercase English letters and asterisks (*), and a name is a string consisting of only uppercase English letters. A pattern p matches a name m if there is a way of replacing every asterisk in p with a (possibly empty) string to obtain m. Notice that each asterisk may be replaced by a different string.
Given N patterns, can you find a single name of at most 104 letters that matches all those patterns at once, or report that it cannot be done?
分析
我这题做了快两个小时,还没AC,心态崩了
解题关键是分析好题目描述和样例,再想一些样例出来证明自己的猜想
当时只想到了是最长前缀和后缀,但不会处理多个*的情况
被官方样例骗了,应该自己想一些的,特别是*数量不同的模式串的情况
*B*D*
PPPPPP*ZZZZZZ
ans=PPPPPPBDZZZZZZ
可以发现,内部的*根本没有用,因为内部的模式串都可以用另一个模式串的*完全匹配
所以,我们只需要看头尾两个*外面的字符,判断第一个*前的前缀和最后一个*后的后缀即可
看来还是要先验证自己的想法,再进行编程,不然做多错多。
code
字符串的题,还是用python切片爽
def solve():
n = int(input())
prefix = ''
suffix = ''
ans = ''
mid = ''
for i in range(n):
s = input().split("*")
if ans == '*':
continue
now_prefix = s[0]
now_suffix = s[-1]
if (len(s) > 2):
for i in range(1, len(s)-1):
mid += s[i]
len_prefix = min(len(now_prefix), len(prefix))
len_suffix = min(len(now_suffix), len(suffix))
if now_prefix[:len_prefix] == prefix[:len_prefix]:
if len(now_prefix) > len(prefix):
prefix = now_prefix
else:
ans = '*'
if now_suffix[len(now_suffix)-len_suffix:] == suffix[len(suffix)-len_suffix:]:
if len(now_suffix) > len(suffix):
suffix = now_suffix
else:
ans = '*'
if ans != '*':
ans = prefix+mid+suffix
print(ans)
T = int(input())
for t in range(1, T+1):
print("Case #{}: ".format(t), end='')
solve()
Pascal Walk
在杨辉三角上面走,从杨辉三角的顶部开始,使经过的数的和等于一个给定的值$N<=10^9$,求该路径
分析
N的范围这么大,肯定不是常规方法啊,绝对要用到数学性质
这题没多少时间想,当时想到了杨辉三角的一个重要性质:第i行所有数的和为$2^{i-1}$
可以对N进行二进制分解,看看要走哪些行才能得到N
但是又不能只走这些行,中间不走的那些行,经过一次起码加1,怎么办呢?
反正当时比赛的时候没想出来,在那里画来画去想找规律
思路来自
$2^{30}>1e9$,那么用前30行(第三十行的和为2^{29})肯定能够表示N了
从第一行开始,虽然(1,1)是必取的,但如果n-=30后,n的二进制最低位是1的话,是要在30行后补上一行的
默认每一行都不取,n-=30后,再看n的二进制每一位上是否为1,是的话就取该层,输出该层的位置,并且要在30行后面补上一行(只有一个1),不是的话就输出边上的位置
非常巧妙的一种方法,避免了枚举哪些行是不取的
code
#include <iostream>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;
void solve()
{
int n;
cin >> n;
if (n <= 500)
{
for (int i = 1; i <= n; i++)
{
printf("%d 1\n", i);
}
return;
}
n -= 30;
bool start_from_left = 1;
int extra_row = 0;
// row要从1开始
for (int row = 1; row <= 30; row++)
{
if (start_from_left)
{
printf("%d 1\n", row);
}
else
{
printf("%d %d\n", row, row);
}
if (n & 1)
{
if (start_from_left)
{
for (int j = 2; j <= row; j++)
{
printf("%d %d\n", row, j);
}
}
else
{
for (int j = row - 1; j >= 1; j--)
{
printf("%d %d\n", row, j);
}
}
++extra_row;
start_from_left = !start_from_left;
}
n >>= 1;
}
for (int i = 31; i <= extra_row + 30; i++)
{
if (start_from_left)
{
printf("%d 1\n", i);
}
else
{
printf("%d %d\n", i, i);
}
}
}
int main()
{
int T;
cin >> T;
cin.ignore();
for (int caseNum = 1; caseNum <= T; caseNum++)
{
printf("Case #%d:\n", caseNum);
solve();
}
return 0;
}
4.12 Notes
4.6-4.12 Learning Notes
Leetcode
两种缓存算法
- LRU
- LFU
LRU: Least Recently Used
获取键 / 检查键是否存在
设置键
删除最先插入的键
分析
既然要$O(1)$时间内完成,那肯定要用哈希表
只用哈希表只能实现get(key)功能,还要存储每个key的使用次数的话,就要加上双向链表
哈希表和双向链表应该怎么结合(套)在一起呢?
From here
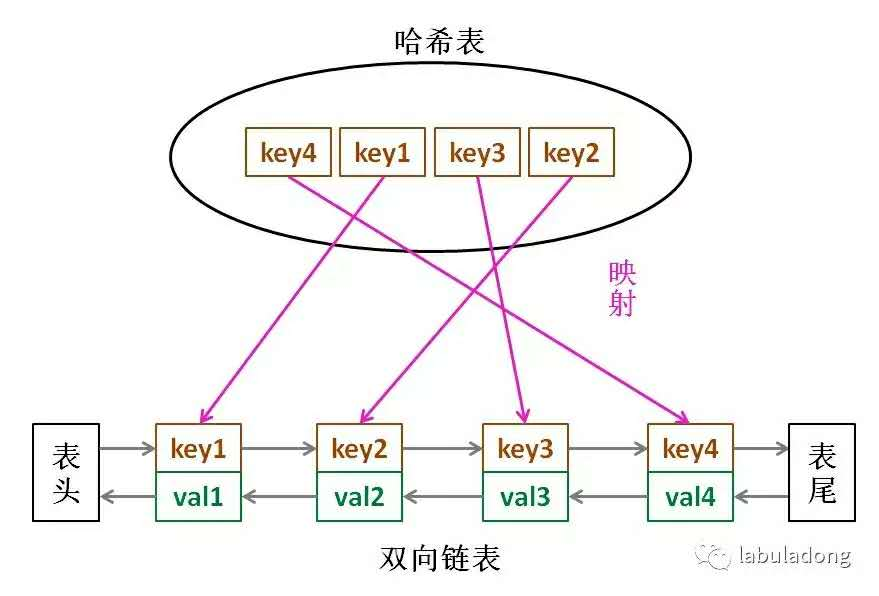
“那么,什么数据结构同时符合上述条件呢?哈希表查找快,但是数据无固定顺序;链表有顺序之分,插入删除快,但是查找慢。所以结合一下,形成一种新的数据结构:哈希链表。”
哈希表里面的value存储的是双向链表中的节点node,双向链表中按访问时间由近到远排序。
每次get就更新key对应的node顺序,把node放到双向链表的头部。
每次put的时候,都要把当前节点now放到双向链表的头部,如果找不到key,就插入key,如果找到key,就更新value。如果插入新的key时缓存满了,就把双向链表的尾部丢掉。
code
手写双向链表+unordered_map
- 初始化
nullptr lift_now_to_head把now节点插入到链表头部unordered_map直接用下标访问m[key]m.erase(last->key)+delete last释放空间
#include <vector>
#include <algorithm>
#include <iostream>
#include <unordered_map>
using namespace std;
class MyListNode
{
public:
int key;
int val;
MyListNode *pre;
MyListNode *nxt;
MyListNode(int k, int v)
{
key = k;
val = v;
pre = nullptr;
nxt = nullptr;
}
};
class LRUCache
{
public:
MyListNode *head;
MyListNode *tail;
unordered_map<int, MyListNode *> m;
int cap;
int now_size;
LRUCache(int capacity)
{
now_size = 0;
cap = capacity;
head = new MyListNode(-1, -1);
tail = new MyListNode(-1, -1);
head->nxt = tail;
tail->pre = head;
}
void lift_now_to_head(MyListNode *now)
{
if (now->pre != nullptr && now->nxt != nullptr)
{
now->pre->nxt = now->nxt;
now->nxt->pre = now->pre;
}
now->nxt = head->nxt;
now->pre = head;
head->nxt->pre = now;
head->nxt = now;
}
int get(int key)
{
if (m.find(key) == m.end())
{
return -1;
}
MyListNode *now = m[key];
lift_now_to_head(now);
return now->val;
}
void put(int key, int value)
{
MyListNode *now;
if (m.find(key) == m.end())
{
now = new MyListNode(key, value);
if (now_size < cap)
{
now_size++;
m[key] = now;
}
else
{
MyListNode *last = tail->pre;
last->pre->nxt = tail;
tail->pre = last->pre;
m.erase(last->key);
delete last;
m[key] = now;
}
}
else
{
now = m[key];
now->val = value;
}
lift_now_to_head(now);
}
};
LFU: Least Frequently Used
From here:
本题其实就是在LRU的基础上,在删除策略里多考虑了一个维度(「访问次数」)的信息。”
核心思想:先考虑访问次数,在访问次数相同的情况下,再考虑缓存的时间。
题解
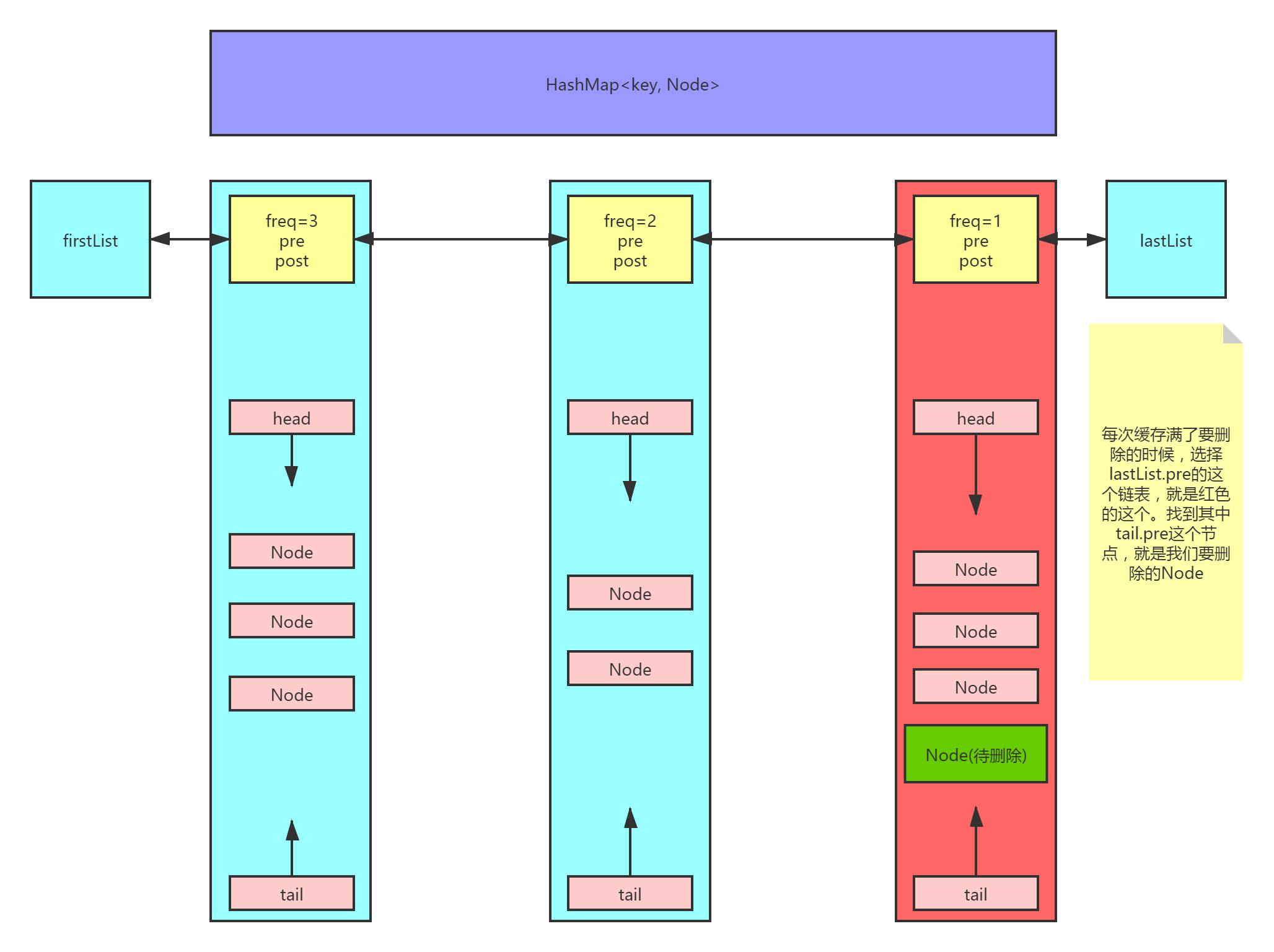
1个哈希表+2个双向链表
- 哈希表
time_map:key-NodeNode里面存valuefreqfreq_node - 双向链表
FreqListNode:按访问次数从大到小排列 - 双向链表
TimeListNode:按访问时间从近到远排列(LRU中的双向链表)
P.S.先声明两个classFreqListNode和TimeListNode,就可以互相引用了
get:
直接访问key对应的TimeListNode获取value,并更新当前TimeListNode的freq,把当前TimeListNode放到的下一个FreqListNode上put:
key存在,更新value和freq,更新freq要把TimeListNode取出来放到下一个FreqListNode上key不存在- 缓存满了:删掉
freq最小且访问时间最远的节点,即为FreqList的尾部的TimeList尾部,然后进行2.ii - 缓存没满:插入新节点,放在
freq=1的FreqListNode上的头部
- 缓存满了:删掉
code
满满的,都是坑啊
手写两个双向链表是非常好的锻炼机会[狗头]
#include <unordered_map>
using namespace std;
const int INF = 1 << 30;
// first declare
class FreqListNode;
class TimeListNode;
class TimeListNode
{
public:
int key;
int val;
int freq;
TimeListNode *pre;
TimeListNode *nxt;
FreqListNode *freq_node;
TimeListNode(int k, int v)
{
key = k;
val = v;
freq = 1;
freq_node = nullptr;
pre = nullptr;
nxt = nullptr;
}
};
class FreqListNode
{
public:
int freq;
FreqListNode *pre;
FreqListNode *nxt;
TimeListNode *time_head;
TimeListNode *time_tail;
FreqListNode(int f)
{
freq = f;
pre = nullptr;
nxt = nullptr;
time_head = new TimeListNode(-1, -1);
time_tail = new TimeListNode(-1, -1);
time_head->nxt = time_tail;
time_tail->pre = time_head;
}
};
class LFUCache
{
public:
FreqListNode *freq_head;
FreqListNode *freq_tail;
unordered_map<int, TimeListNode *> time_map;
int cap;
int now_size;
LFUCache(int capacity)
{
now_size = 0;
cap = capacity;
freq_head = new FreqListNode(INF);
freq_tail = new FreqListNode(0);
freq_head->nxt = freq_tail;
freq_tail->pre = freq_head;
}
void erase_empty_FreqListNode(FreqListNode *now_freq)
{
if (now_freq->time_head->nxt == now_freq->time_tail)
{
now_freq->pre->nxt = now_freq->nxt;
now_freq->nxt->pre = now_freq->pre;
delete now_freq;
}
}
void incre_freq(TimeListNode *now)
{
now->pre->nxt = now->nxt;
now->nxt->pre = now->pre;
now->freq += 1;
FreqListNode *now_freq = now->freq_node;
FreqListNode *nxt_freq = now_freq->pre;
if (nxt_freq->freq > now->freq)
{
nxt_freq = new FreqListNode(now->freq);
now_freq->pre->nxt = nxt_freq;
nxt_freq->pre = now_freq->pre;
nxt_freq->nxt = now_freq;
now_freq->pre = nxt_freq;
}
now->freq_node = nxt_freq;
lift_now_to_head(now);
erase_empty_FreqListNode(now_freq);
}
void insert_TimeListNode(TimeListNode *now)
{
FreqListNode *now_freq;
if (freq_tail->pre != nullptr && freq_tail->pre->freq == 1)
{
now_freq = freq_tail->pre;
}
else
{
now_freq = new FreqListNode(1);
freq_tail->pre->nxt = now_freq;
now_freq->pre = freq_tail->pre;
now_freq->nxt = freq_tail;
freq_tail->pre = now_freq;
}
now->freq_node = now_freq;
now->freq = 1;
TimeListNode *time_head = now_freq->time_head;
time_head->nxt->pre = now;
now->nxt = time_head->nxt;
now->pre = time_head;
time_head->nxt = now;
}
void delete_last_TimeListNode()
{
FreqListNode *now_freq_node = freq_tail->pre;
TimeListNode *time_tail = now_freq_node->time_tail;
TimeListNode *now = time_tail->pre;
time_map.erase(now->key);
now->pre->nxt = time_tail;
time_tail->pre = now->pre;
delete now;
erase_empty_FreqListNode(now_freq_node);
}
void lift_now_to_head(TimeListNode *now)
{
FreqListNode *now_freq = now->freq_node;
TimeListNode *head = now_freq->time_head;
TimeListNode *tail = now_freq->time_tail;
now->nxt = head->nxt;
now->pre = head;
head->nxt->pre = now;
head->nxt = now;
}
int get(int key)
{
if (time_map.find(key) == time_map.end())
{
return -1;
}
TimeListNode *now = time_map[key];
incre_freq(now);
return now->val;
}
void put(int key, int value)
{
TimeListNode *now;
if (!cap)
return;
if (time_map.find(key) == time_map.end())
{
now = new TimeListNode(key, value);
if (now_size < cap)
{
now_size++;
time_map[key] = now;
insert_TimeListNode(now);
}
else
{
delete_last_TimeListNode();
time_map[key] = now;
insert_TimeListNode(now);
}
}
else
{
now = time_map[key];
now->val = value;
incre_freq(now);
}
}
};
4.5 Notes
3.30-4.5 Learning Notes
python unpacking
create a list using range
>>> l=[*range(1,10)]
>>> l
[1, 2, 3, 4, 5, 6, 7, 8, 9]
combine 2 lists
>>> list1 = [1,2,3]
>>> list2 = range(3,6)
>>> [*list1, *list2]
[1, 2, 3, 3, 4, 5]
combine 2 dictionaries
>>> a = {"a":1, "b":2}
>>> b = {"c":3, "d":4}
>>> {**a, **b}
{'a': 1, 'b': 2, 'c': 3, 'd': 4}
Leetcode
惯性思维害死人
每 3 个士兵可以组成一个作战单位,分组规则如下:
从队伍中选出下标分别为 i、j、k 的 3 名士兵,他们的评分分别为 rating[i]、rating[j]、rating[k]
作战单位需满足:
$rating[i] < rating[j] < rating[k]$ or $rating[i] > rating[j] > rating[k]$
$0 <= i < j < k < n$
一开始我想到了这是一种偏序关系,是不是可以用LIS来求呢?
于是走上了一条不归之路……
等价于求一个数列中,长度为3的递增序列个数
- 一开始想,这不是很简单吗?直接套LIS模板,长度为3的递增序列个数=${LISLength}\choose{3}$。交的时候发现不对劲,因为LIS可能有多个。
- 然后就套求LIS个数的模板了,但这样也是错的
- 要不我们求长度等于LISLength的所有递增序列中出现过的元素个数$tot$,答案是${tot}\choose{3}$,转移的时候还要带上路径。
估计一下这样做的时间复杂度:
$O(n^2)$求LIS,$O(nk)$求出现过的元素个数,其中$k=LISLengthLISNumber$
总的时间复杂度为$O(n^2)$
看起来没问题,但其实问题很大:
__长度为3的递增序列__可以不出现在LIS中
e.g.
1 1000 1001 2 3 4 5 6
(1,1000,1001)就没有出现在LIS(1,2,3,4,5,6)中
所以这题跟LIS一点关系都没有!
我还是去看官方题解吧
- 暴力枚举三个数看它们是否满足关系$O(n^3)$
- 枚举中间的数,求左侧比它大/小的元素的个数,求右侧比它大/小的元素的个数$O(n^2)$
- 离散化树状数组优化第二种方法$O(nlogn)$
第二种方法的代码:
#include <vector>
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;
class Solution
{
public:
int numTeams(vector<int> &rating)
{
int ans = 0;
int n = rating.size();
if (n < 3)
return 0;
for (int i = 1; i < rating.size() - 1; i++)
{
int left_less_num = 0;
int left_bigger_num = 0;
int right_less_num = 0;
int right_bigger_num = 0;
for (int j = 0; j < i; j++)
{
if (rating[j] > rating[i])
{
left_bigger_num++;
}
else if (rating[j] < rating[i])
{
left_less_num++;
}
}
for (int j = i + 1; j < rating.size(); j++)
{
if (rating[j] > rating[i])
{
right_bigger_num++;
}
else if (rating[j] < rating[i])
{
right_less_num++;
}
}
ans += left_less_num * right_bigger_num + left_bigger_num * right_less_num;
}
return ans;
}
};
惯性思维害死人啊啊啊啊!!!!
逐步优化算法
不要怕自己一开始想出来的算法太慢$O(n^2)/O(n^3)$
先保证能得到答案,然后再一步一步地优化。
详见该题解
作者:windliang
链接:https://leetcode-cn.com/problems/trapping-rain-water/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/
- 按行求:就是先求高度为 1 的水,再求高度为 2 的水,再求高度为 3 的水。
- 按列求:求每一列的水,我们只需要关注当前列,以及左边最高的墙,右边最高的墙就够了。
- 优化第二种按列求的方法,发现不需要都用$O(n)$时间去找两边最高的墙,可以用两个数组预处理,算出第$i$列两边最高的墙
- 优化第三种方法,把两个数组压掉,降低空间复杂度。因为这两个数组中的元素我们只用一次,所以可以用两个变量来代替
- 用栈来模拟接雨水的过程:当遍历墙的高度的时候,如果当前高度小于栈顶的墙高度,说明这里会有积水,我们将墙的高度的下标入栈。如果当前高度大于栈顶的墙的高度,说明之前的积水到这里停下,我们可以计算下有多少积水了。计算完,就把当前的墙继续入栈,作为新的积水的墙。当遍历墙的高度的时候,如果当前高度小于栈顶的墙高度,说明这里会有积水,我们将墙的高度的下标入栈。
3.29 Notes
3.23-3.29 Learning Notes
Leetcode
使数组唯一的最小增量
- 排序+贪心
- 计数排序
- 线性探测+路径压缩
排序+贪心
先从小到大排序,然后遍历每个数
如果当前数小于等于上一个数,就把当前数补齐到上一个数+1
计数排序
class Solution
{
public:
int bucket[80005];
int minIncrementForUnique(vector<int> &A)
{
if (A.size() <= 1)
return 0;
int ans = 0;
int maxn = 0;
for (auto each : A)
{
bucket[each]++;
maxn = max(maxn, each);
}
for (int i = 0; i <= maxn; i++)
{
if (bucket[i] >= 2)
{
ans += bucket[i] - 1;
bucket[i + 1] += bucket[i] - 1;
}
}
if (bucket[maxn + 1] >= 2)
{
int n = bucket[maxn + 1] - 1;
ans += (1 + n) * n / 2;
}
return ans;
}
};
线性探测+路径压缩
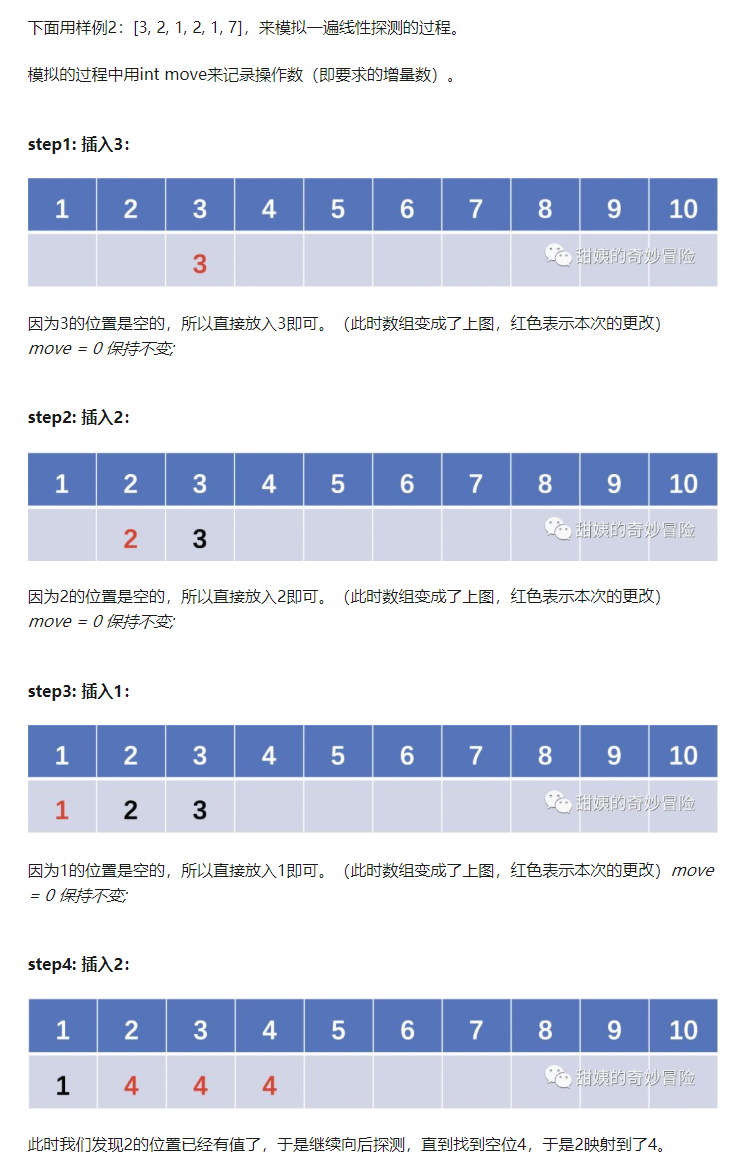
这道题换句话说,就是需要把原数组映射到一个地址不冲突的区域,映射后的地址不小于原数组对应的元素。
比如[3, 2, 1, 2, 1, 7]就映射成了[3, 2, 1, 4, 5, 7]。
我想了下,这道题目其实和解决hash冲突的线性探测法比较相似!
如果地址冲突了,会探测它的下一个位置,如果下一个位置还是冲突,继续向后看,直到第一个不冲突的位置为止。
没有路径压缩的版本:
class Solution
{
public:
int hash[80005];
int find(int pos)
{
while (hash[pos] != -1)
{
++pos;
}
return pos;
}
int minIncrementForUnique(vector<int> &A)
{
int ans = 0;
memset(hash, -1, sizeof(hash));
for (auto each : A)
{
if (hash[each] == -1)
{
hash[each] = each;
}
else
{
int pos = find(each);
hash[pos] = each;
ans += pos - each;
}
}
return ans;
}
};
怎么路径压缩呢?就是经过某条路径最终探测到一个空位置x后,将这条路径上的值都变成空位置所在的下标x,那么假如下次探测的点又是这条路径上的点,则可以直接跳转到这次探测到的空位置x,从x开始继续探测。
这里的路径压缩有点像并查集里面的路径压缩,但是有一点点不同,找到空位置后要给它赋值
int find(int pos)
{
if (hash[pos] == -1)
{
hash[pos] = pos;
return pos;
}
hash[pos] = find(hash[pos] + 1);
return hash[pos];
}
#include <vector>
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;
class Solution
{
public:
int hash[80005];
int minIncrementForUnique(vector<int> &A)
{
int ans = 0;
memset(hash, -1, sizeof(hash));
for (auto each : A)
{
if (hash[each] == -1)
{
hash[each] = each;
}
else
{
int pos = find(each);
ans += pos - each;
}
}
return ans;
}
};
dp: 打家劫舍x3
I
解题思路
f[i][0]表示前i个预约,其中第i个预约不接的最大值f[i][0]表示前i个预约,其中第i个预约接的最大值
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + nums[i - 1];
注意到f[i]只依赖与前一个状态f[i-1],所以我们可以不用数组,只用两个变量存储前一个状态
代码
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
// int f[2005][2];
int massage(vector<int> &nums)
{
int n = nums.size();
int preRest = 0, preWork = 0;
int nowRest = 0, nowWork = 0;
for (int i = 1; i <= n; i++)
{
nowRest = max(preRest, preWork);
nowWork = preRest + nums[i - 1];
preRest = nowRest;
preWork = nowWork;
// f[i][0] = max(f[i - 1][0], f[i - 1][1]);
// f[i][1] = f[i - 1][0] + nums[i - 1];
}
return max(nowRest, nowWork);
// return max(f[n][0], f[n][1]);
}
};
II
环形:第一个房子和最后一个不能同时取
所以有两种情况:
- 不取第一个
- 不取最后一个
最后取两种情况的最大值即可
class Solution
{
public:
// int f[2005][2];
int rob(vector<int> &nums)
{
int n = nums.size();
if (n == 0)
{
return 0;
}
if (n == 1)
return nums[0];
int preRest = 0, preWork = 0;
int nowRest = 0, nowWork = 0;
for (int i = 1; i < n; i++)
{
nowRest = max(preRest, preWork);
nowWork = preRest + nums[i - 1];
preRest = nowRest;
preWork = nowWork;
}
int ans = max(preRest, preWork);
preRest = 0, preWork = 0;
for (int i = 2; i < n; i++)
{
nowRest = max(preRest, preWork);
nowWork = preRest + nums[i - 1];
preRest = nowRest;
preWork = nowWork;
}
nowWork = preRest + nums[n - 1];
ans = max(ans, nowWork);
return ans;
}
};
III
树形:孩子和父亲不能同时取
思路是类似的,注意preWork不一样,有三种情况:
- 左右都取
- 取左不取右
- 取右不取左
class Solution
{
public:
pair<int, int> dfs(TreeNode *now)
{
if (now == NULL)
return make_pair(0, 0);
pair<int, int> le = dfs(now->left);
pair<int, int> ri = dfs(now->right);
int preRest = le.first + ri.first;
int preWork = max(le.first + ri.second, max(le.second + ri.first, le.second + ri.second));
int nowWork = preRest + now->val;
int nowRest = max(preRest, preWork);
return make_pair(nowRest, nowWork);
}
int rob(TreeNode *root)
{
pair<int, int> ans = dfs(root);
return max(ans.first, ans.second);
}
};
Trie
Trie模板
class Trie
{
private:
bool isEnd;
Trie *nxt[26];
public:
/** Initialize your data structure here. */
Trie()
{
isEnd = false;
for (int i = 0; i < 26; i++)
nxt[i] = nullptr;
}
/** Inserts a word into the trie. */
void insert(string word)
{
Trie *node = this;
for (char ch : word)
{
if (!node->nxt[ch - 'a'])
node->nxt[ch - 'a'] = new Trie();
node = node->nxt[ch - 'a'];
}
node->isEnd = true;
}
/** Returns if the word is in the trie. */
bool search(string word)
{
Trie *node = this;
for (char ch : word)
{
if (!node->nxt[ch - 'a'])
return false;
node = node->nxt[ch - 'a'];
}
return node->isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix)
{
Trie *node = this;
for (char ch : prefix)
{
if (!node->nxt[ch - 'a'])
return false;
node = node->nxt[ch - 'a'];
}
return true;
}
};
Trie匹配后缀
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 “#” 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
题目分析
要让索引字符串长度最小,就要尽量利用单词的公共部分。
一个单词时另一个单词的前缀时,不能缩短索引字符串长度
bell
be
be#bell#
发现只有一个单词是另一个单词的后缀时,才能缩短索引字符串长度
time
me
time#
所以,对于每一个单词,我们希望找到以它为后缀的另一个单词,如果能找到,就能够将这两个单词叠加起来,不需要增加额外长度。
暴力$O(n^2)$
先按单词长度从大到小排序,从第二个单词开始遍历,判断当前单词是否为之前的某一个单词(长度大于等于当前单词)的后缀
如果是,索引字符串长度不变
如果不是,索引字符串长度加上当前单词长度再加1word#
class Solution
{
public:
static bool cmp(string a, string b)
{
return a.length() > b.length();
}
int minimumLengthEncoding(vector<string> &words)
{
int ans = 0;
sort(words.begin(), words.end(), cmp);
ans += words[0].length() + 1;
for (int i = 1; i < words.size(); i++)
{
// cout << words[i] << endl;
bool ismatch = 0;
int len = words[i].size();
for (int j = i - 1; j >= 0; j--)
{
if (words[j].compare(words[j].size() - len, len, words[i]) == 0)
{
ismatch = 1;
break;
}
}
if (!ismatch)
{
ans += len + 1;
}
}
return ans;
}
};
Trie $O(?)$ 反正比暴力快
求一个单词的后缀=求这个单词反过来之后的前缀
这不是可以用Trie吗?
还是要先按单词长度从大到小排序,再将倒置的单词一个个加入到Trie中
如果不这么做,me先被加到树中,不能被time匹配到
如果当前单词是某一单词的前缀,那么当前单词肯定在Trie中
如果不是,就更新Trie
class Trie
{
private:
bool isEnd;
Trie *nxt[26];
public:
Trie()
{
isEnd = false;
for (int i = 0; i < 26; i++)
{
nxt[i] = nullptr;
}
}
bool searchPrefixAndInsert(string s)
{
auto node = this;
bool match = 1;
for (auto ch : s)
{
if (!node->nxt[ch - 'a'])
{
node->nxt[ch - 'a'] = new Trie;
match = 0;
}
node = node->nxt[ch - 'a'];
}
return match;
}
};
class Solution
{
public:
static bool cmp(string a, string b)
{
return a.size() > b.size();
}
int minimumLengthEncoding(vector<string> &words)
{
Trie *root = new Trie();
int ans = 0;
sort(words.begin(), words.end(), cmp);
for (auto word : words)
{
reverse(word.begin(), word.end());
if (!root->searchPrefixAndInsert(word))
ans += word.size() + 1;
}
return ans;
}
};
Trie上搜索
search(word) 可以搜索文字或正则表达式字符串,字符串只包含字母 . 或 a-z 。 . 可以表示任何一个字母。
.可以表示任何一个字母,遇到到.的时候怎么办?
遇到.表示可以通向任何一个连接的字母node->nxt[j] if node->nxt[j]!=nullptr
接着搜索剩下的字符串word.substr(i+1)
只要至少一个分支匹配成功,就算成功isMatch|=
this指向当前引用的对象
所以需要用node->nxt[j]->search来引用node->nxt[j]
for (int j = 0; j < 26; j++)
{
if (node->nxt[j])
{
isMatch |= node->nxt[j]->search(word.substr(i + 1));
}
}
code
class WordDictionary
{
public:
bool isEnd;
WordDictionary *nxt[26];
WordDictionary()
{
isEnd = 0;
for (int i = 0; i < 26; i++)
nxt[i] = nullptr;
}
void addWord(string word)
{
auto node = this;
for (auto ch : word)
{
if (!node->nxt[ch - 'a'])
{
node->nxt[ch - 'a'] = new WordDictionary;
}
node = node->nxt[ch - 'a'];
}
node->isEnd = 1;
}
bool search(string word)
{
auto node = this;
for (int i = 0; i < word.size(); i++)
{
if (word[i] == '.')
{
// . can represent any word exist
bool isMatch = 0;
for (int j = 0; j < 26; j++)
{
if (node->nxt[j])
{
isMatch |= node->nxt[j]->search(word.substr(i + 1));
}
}
return isMatch;
}
node = node->nxt[word[i] - 'a'];
if (!node)
return false;
}
return node->isEnd;
}
};
Trie+回溯
三种解法:
- 暴搜
- Trie+回溯,结合程度低
- Trie+回溯,结合程度高
暴搜TLE
枚举每个在字典中的单词,枚举每个出发点
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int dire[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, m;
bool visited[105][105];
vector<string> ans;
bool match;
void dfs(int x, int y, string nowWord, string finalWord, vector<vector<char>> &board)
{
if (match)
return;
if (nowWord == finalWord)
{
ans.push_back(nowWord);
match = 1;
return;
}
visited[y][x] = 1;
for (auto dir : dire)
{
int nxt_x = x + dir[0];
int nxt_y = y + dir[1];
if (nxt_x >= 0 && nxt_x < m && nxt_y >= 0 && nxt_y < n)
{
if (!visited[nxt_y][nxt_x])
{
char nxt_ch = finalWord[nowWord.size()];
if (board[nxt_y][nxt_x] == nxt_ch)
{
string nxtWord = nowWord + nxt_ch;
dfs(nxt_x, nxt_y, nxtWord, finalWord, board);
visited[nxt_y][nxt_x] = 0;
}
}
}
}
}
vector<string> findWords(vector<vector<char>> &board, vector<string> &words)
{
n = board.size();
m = board[0].size();
for (auto word : words)
{
match = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (board[i][j] == word[0])
{
string nxtWord(1, word[0]);
dfs(j, i, nxtWord, word, board);
visited[i][j] = 0;
}
if (match)
break;
}
if (match)
break;
}
}
return ans;
}
};
结合不紧密的Trie+回溯
基本等于在暴搜的基础上加上Trie模板
用Trie来帮助暴搜剪枝
- 不需要枚举每个在字典中的单词,直接搜索当前单词是否在字典中即可
- 搜索当前单词是否是字典中某个单词的前缀,如果不是就可以剪枝
return
这里有个很容易错的小细节:
找到匹配的单词后不能return,因为可能有以当前单词为前缀的其他单词,如果return就不能找到它们了
e.g.
dict={"ab","abc"}
board={"a","b","c"}
如果找到"ab"的时候直接return,"abc"就永远不可能被匹配到
另外一个优化的点:
题意只需要求出现的单词,不要重复的,与其用unordered_map这类东西来去重,不如直接在Trie中改动一下。
在匹配单词的函数中这样写,就能使每个单词只出现一次。
if (node->isEnd)
{
node->isEnd = 0;
return true;
}
if (root->searchWord(nowWord))
{
ans.push_back(nowWord);
// return;
}
if (!root->startWith(nowWord))
{
return;
}
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Trie
{
public:
bool isEnd;
Trie *nxt[26];
Trie()
{
isEnd = 0;
for (int i = 0; i < 26; i++)
{
nxt[i] = nullptr;
}
}
void insert(string word)
{
Trie *node = this;
for (char each : word)
{
if (!node->nxt[each - 'a'])
{
node->nxt[each - 'a'] = new Trie();
}
node = node->nxt[each - 'a'];
}
node->isEnd = 1;
}
bool startWith(string word)
{
Trie *node = this;
for (char each : word)
{
if (!node->nxt[each - 'a'])
{
return false;
}
node = node->nxt[each - 'a'];
}
return true;
}
bool searchWord(string word)
{
Trie *node = this;
for (char each : word)
{
if (!node->nxt[each - 'a'])
{
return false;
}
node = node->nxt[each - 'a'];
}
// find the word and delete it
if (node->isEnd)
{
node->isEnd = 0;
return true;
}
return false;
}
};
class Solution
{
public:
int dire[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, m;
bool visited[105][105];
Trie *root;
vector<string> ans;
void dfs(int x, int y, string nowWord, vector<vector<char>> &board)
{
if (root->searchWord(nowWord))
{
ans.push_back(nowWord);
// return;
}
if (!root->startWith(nowWord))
{
return;
}
for (auto dir : dire)
{
int nxt_x = x + dir[0];
int nxt_y = y + dir[1];
if (nxt_x >= 0 && nxt_x < n && nxt_y >= 0 && nxt_y < m)
{
if (!visited[nxt_x][nxt_y])
{
string nxtWord = nowWord + board[nxt_x][nxt_y];
visited[nxt_x][nxt_y] = 1;
dfs(nxt_x, nxt_y, nxtWord, board);
visited[nxt_x][nxt_y] = 0;
}
}
}
}
vector<string> findWords(vector<vector<char>> &board, vector<string> &words)
{
n = board.size();
m = board[0].size();
root = new Trie();
for (auto word : words)
{
root->insert(word);
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
string nowWord(1, board[i][j]);
visited[i][j] = 1;
dfs(i, j, nowWord, board);
visited[i][j] = 0;
}
}
return ans;
}
};
结合紧密的Trie+回溯
推荐看这位大佬用hashmap的题解以及下面评论区使用一般前缀树的代码
有了Trie,怎么进一步优化我们的搜索回溯呢?
答案就是直接把Trie的节点作为一个状态,放到搜索里面。
- 判断单词是否匹配? 看
now->isEnd==1 - 判断当前字符串是否是某一单词的前缀? 看
now->nxt[board[x][y] - 'a'] == nullptr - 下一个位置的字符串是?
now = now->nxt[board[x][y] - 'a']
另外,这里的搜索写法与之前差别比较大,而且把visited[][]砍掉了。
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Trie
{
public:
bool isEnd;
Trie *nxt[26];
string word;
Trie()
{
isEnd = 0;
for (int i = 0; i < 26; i++)
{
nxt[i] = nullptr;
}
word = "";
}
void insert(string word)
{
Trie *node = this;
for (char each : word)
{
if (node->nxt[each - 'a'] == nullptr)
{
node->nxt[each - 'a'] = new Trie();
}
node = node->nxt[each - 'a'];
}
node->isEnd = 1;
node->word = word;
}
};
class Solution
{
public:
vector<string> ans;
void dfs(Trie *now, int x, int y, vector<vector<char>> &board)
{
if (now->isEnd)
{
now->isEnd = 0;
ans.push_back(now->word);
return;
}
if (x < 0 || x >= board.size() || y < 0 || y >= board[0].size())
return;
if (board[x][y] == '#')
return;
if (now->nxt[board[x][y] - 'a'] == nullptr)
return;
now = now->nxt[board[x][y] - 'a'];
char cur = board[x][y];
board[x][y] = '#';
dfs(now, x + 1, y, board);
dfs(now, x - 1, y, board);
dfs(now, x, y + 1, board);
dfs(now, x, y - 1, board);
board[x][y] = cur;
}
vector<string> findWords(vector<vector<char>> &board, vector<string> &words)
{
Trie *root = new Trie();
for (auto word : words)
{
root->insert(word);
}
for (int i = 0; i < board.size(); i++)
{
for (int j = 0; j < board[0].size(); j++)
{
dfs(root, i, j, board);
}
}
return ans;
}
};
这道题的一些延伸思考
nullptr
c++11 推出的东东,表示一个空指针
反正记住比null好用就对了
a[x][y]ora[y][x]
在数学里面,(x,y)看起来更顺眼哎
但是如果我们把数学里面的坐标系放到二维数组中来看,发现有点不对劲
a=[ 1 2 3
1 [1,2,3],
2 [4,5,6],
3 [7,8,9]
]
如果按照数学中的坐标系,第y行第x列对应的数组元素是a[y][x]
但是y在x前面又有点不太舒服,a[x][y]看起来更自然
其实两种写法都可以,关键是你要想明白x代表的是行数或是列数
现在发现a[x][y]更好一点,因为很多时候函数返回值是(x,y),unpack不容易出错
搜索回溯的不同写法
- 先进入下一个状态再判断合法性
- 先判断下一个状态的合法性再进入
个人感觉各有千秋吧
第一种写法代码会更简洁,而且不用考虑dfs(0,0)搜索入口的状态
第二种写法递归调用会少一点,效率会高?(不太清楚)但是要考虑搜索入口的状态
以该题为例:
第一种写法的搜索入口
dfs(root, i, j, board);
第二种写法的搜索入口
string nowWord(1, board[i][j]);
visited[i][j] = 1;
dfs(i, j, nowWord, board);
visited[i][j] = 0;
第一种写法逻辑确实清晰很多,递归边界直接用if return就可以,增减逻辑都方便
多源最短路
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的陆地区域的曼哈顿距离。
单源bfs
- 从每个陆地出发,更新每个海洋到陆地的最短距离
- 从每个海洋出发找离它最近的陆地
这两种单源bfs跑起来都有点慢,需要注意优化常数才能AC,有兴趣的可以看看官方题解中的常数优化
1768 ms 252.5 MB
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
class Solution
{
public:
int dire[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, m;
bool visited[105][105];
vector<vector<int>> a;
struct node
{
int x, y, step;
};
int findNearestIsland(int i, int j)
{
queue<node> q;
memset(visited, 0, sizeof(visited));
visited[i][j] = 1;
q.push({i, j, 0});
while (!q.empty())
{
node now = q.front();
q.pop();
for (int i = 0; i < 4; i++)
{
int nx = now.x + dire[i][0], ny = now.y + dire[i][1];
if (nx < 0 || nx >= n || ny < 0 || ny >= m)
continue;
if (visited[nx][ny])
continue;
// find the nearest island
if (a[nx][ny])
return now.step + 1;
visited[nx][ny] = 1;
q.push({nx, ny, now.step + 1});
}
}
return -1;
}
int maxDistance(vector<vector<int>> &grid)
{
int ans = -1;
n = grid.size();
m = grid[0].size();
a = grid;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (!grid[i][j])
{
ans = max(ans, findNearestIsland(i, j));
}
}
}
return ans;
}
};
多源bfs
先把每个陆地加到队列里面,再一起bfs
多源bfs=以超级源点为第一层,多个选出来的源点为第二层进行bfs
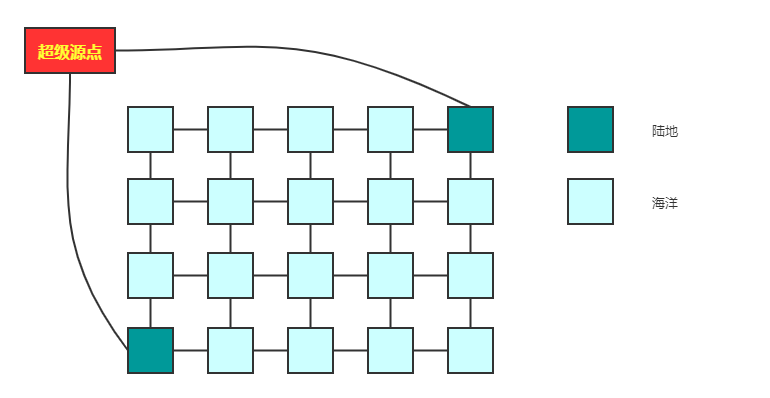
多源bfs明显比单源bfs快很多
324 ms 32.4 MB
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
class Solution
{
public:
int maxDistance(vector<vector<int>> &grid)
{
int dis[105][105];
bool visited[105][105];
int inf = 1 << 30;
for (int x = 0; x < grid.size(); x++)
for (int y = 0; y < grid[0].size(); y++)
visited[x][y] = false;
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[0].size(); j++)
{
dis[i][j] = inf;
}
}
queue<tuple<int, int, int>> q;
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[0].size(); j++)
{
if (grid[i][j])
{
q.push(make_tuple(i, j, 0));
}
}
}
while (!q.empty())
{
auto [x, y, step] = q.front();
q.pop();
if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size())
continue;
if (visited[x][y])
continue;
visited[x][y] = 1;
if (!grid[x][y])
dis[x][y] = min(dis[x][y], step);
// reach another island
if (grid[x][y] && step > 0)
continue;
q.push(make_tuple(x + 1, y, step + 1));
q.push(make_tuple(x - 1, y, step + 1));
q.push(make_tuple(x, y + 1, step + 1));
q.push(make_tuple(x, y - 1, step + 1));
}
int ans = -1;
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[0].size(); j++)
{
if (dis[i][j] == inf)
dis[i][j] = -1;
ans = max(ans, dis[i][j]);
}
}
return ans;
}
};
还可以进一步优化:
- 删掉visited数组,填海造陆,访问过的ocean变成island
- 删掉dis数组,在bfs中记录当前步数(重点)
怎么在bfs中记录当前步数呢?
将问题转化为:怎样在bfs中区分当前层与下一层?
加入一个size变量记录第一次遍历到当前层时的队列长度,即为当前层的元素个数。同一层的步数相等,只有遍历完同一层后才进行step++更新步数。
这样划分层数合理的原因是:队列中同一层的聚在一起,下一层的一定在它们后面
注意最后step-1,因为在判断到队列为空之前,在最后一层bfs中step会多加一次。
优化后效果
112 ms 16.4 MB
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
class Solution
{
public:
int dis[105][105];
int dire[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int maxDistance(vector<vector<int>> &grid)
{
int inf = 1 << 30;
int n = grid.size();
queue<pair<int, int>> q;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (grid[i][j])
{
q.push(make_pair(i, j));
}
}
}
// all islands or all ocean
if (q.size() == n * n || q.size() == 0)
return -1;
int step = 0;
while (!q.empty())
{
int size = q.size();
while (size--)
{
pair<int, int> now = q.front();
int x = now.first;
int y = now.second;
q.pop();
for (int i = 0; i < 4; i++)
{
int nxt_x = x + dire[i][0];
int nxt_y = y + dire[i][1];
if (nxt_x < 0 || nxt_x >= n || nxt_y < 0 || nxt_y >= n)
continue;
if (!grid[nxt_x][nxt_y])
{
// 填海造陆
grid[nxt_x][nxt_y] = 1;
q.push(make_pair(nxt_x, nxt_y));
}
}
}
step++;
}
// why step-1?
// 在最后一层bfs中step会多加一次,在判断到队列为空之前
return step - 1;
}
};
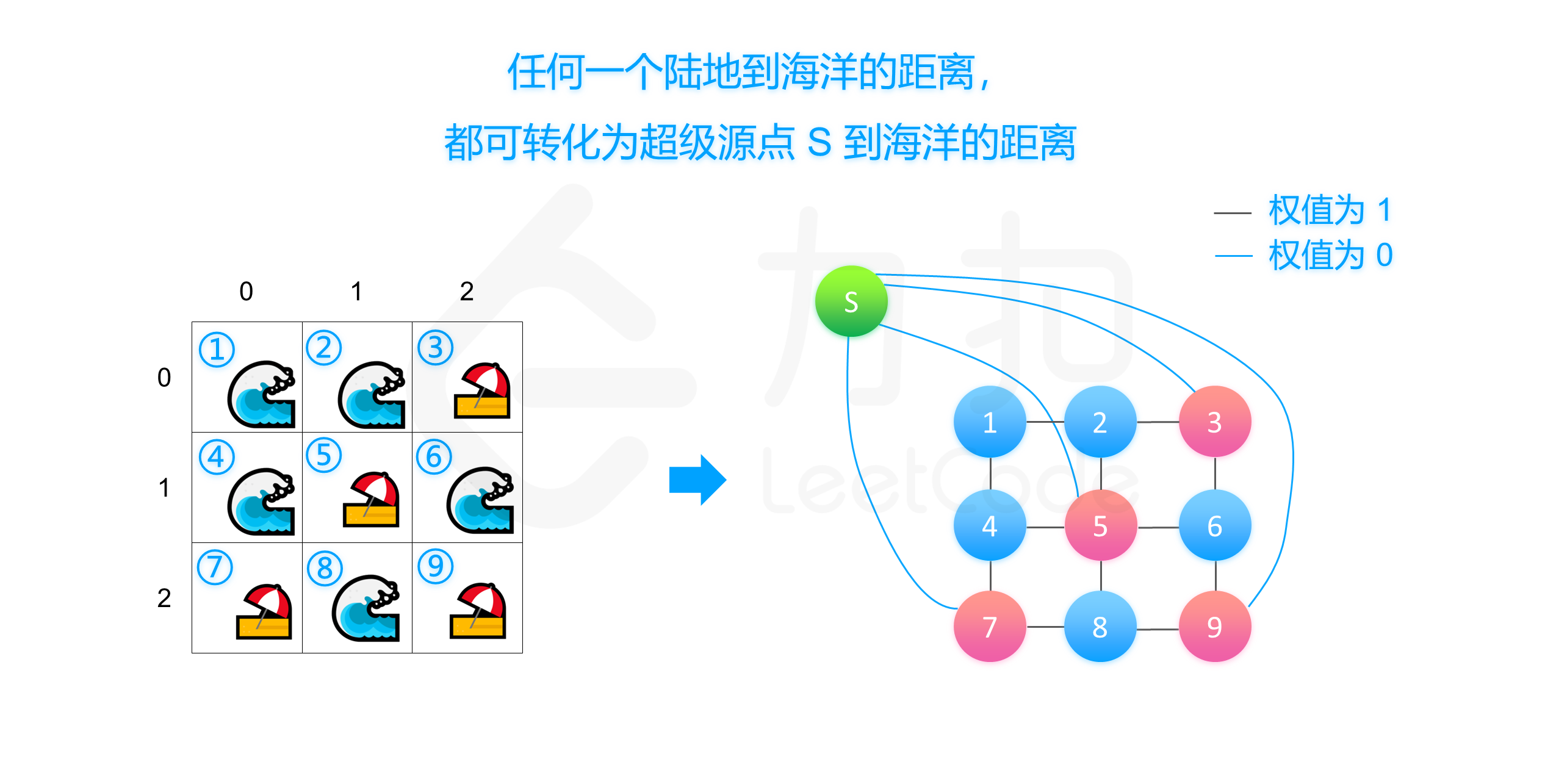
多源最短路
第一次见到dijkstra能用来求多源最短路的
详见官方题解
这里以 Dijkstra 算法为例,我们知道堆优化的 Dijkstra 算法实际上是 BFS 的一个变形,把 BFS 中的队列变成了优先队列,在拓展新状态的时候加入了松弛操作。Dijkstra 的堆优化版本第一步是源点入队,我们只需要把它改成源点集合中的所有的点入队就可以实现求「多源最短路」。
但是根据官方题解的分析,该算法的时间复杂度比多源bfs高
Coding Game
边玩游戏边学编程,何乐而不为?
Clash Of Code
3 modes:
- shortest
- fastest
- reverse
练习编程熟练度,让你的代码更简洁
Contest
几个月会换一次游戏
写程序来玩一个游戏,与其他对手写的程序进行对抗
图形化调试,直接能看到对战录像
慎入,会上瘾
这是一个锻炼自己编程能力的好机会,几百行的代码逻辑,怎么快速定位bug,快速调试
函数/变量命名,代码整合复用,面向对象都能用到
Google Kick Start
Diagonal Puzzle
这题有毒!
我尝试用八皇后的位运算来写这道题,但这道题关键是dfs肯定会超时,要优化算法
3.22 Notes
3.16-3.22 Learning Notes
Leetcode
逆序对
归并排序求逆序对
只需要加上一行代码ans += mid - i + 1;
在合并两个有序数组时,若发现一个逆序对nums[i]>nums[j],则nums[i]>nums[mid+1]~nums[j]且nums[i]~nums[mid]>nums[j]
由于此处j++,j的状态会丢失,所以取这种情况nums[i]~nums[mid]>nums[j]
共mid-i+1个逆序对
code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int ans = 0;
void mergeSort(vector<int> &nums, int left, int right)
{
if (left == right)
{
return;
}
int mid = (left + right) >> 1;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
int i = left, j = mid + 1;
vector<int> sortNums;
while (i <= mid && j <= right)
{
if (nums[i] > nums[j])
{
ans += mid - i + 1;
sortNums.push_back(nums[j++]);
}
else
{
sortNums.push_back(nums[i++]);
}
}
while (i <= mid)
{
sortNums.push_back(nums[i++]);
}
while (j <= right)
{
sortNums.push_back(nums[j++]);
}
for (i = left; i <= right; i++)
{
nums[i] = sortNums[i - left];
}
// cout << left << " " << right << " " << ans << endl;
}
int reversePairs(vector<int> &nums)
{
if (nums.size()<=1)
return 0;
mergeSort(nums, 0, nums.size() - 1);
return ans;
}
};
求LIS个数:O(nlogn)的两种解法(知乎)
1. 用树状数组维护LIS个数
树状数组部分是摘录newhar的题解
class Solution
{
class Node
{
public:
int maxlength, cnt;
Node()
{
maxlength = 1;
cnt = 0;
}
// 区间合并法则
// override: +=
Node operator+=(Node &b)
{
if (b.maxlength == this->maxlength)
{
this->cnt += b.cnt;
}
else if (b.maxlength > this->maxlength)
{
this->maxlength = b.maxlength;
this->cnt = b.cnt;
}
return *this;
}
};
int lowbit(int x)
{
return x & (-x);
}
// 更新一个点后向上更新
void add(Node nodes[], int rank, Node now, int size)
{
for (; rank <= size; rank += lowbit(rank))
{
nodes[rank] += now;
}
}
// 单点查找
Node query(Node nodes[], int rank)
{
Node res;
while (rank)
{
res += nodes[rank];
rank -= lowbit(rank);
}
return res;
}
public:
int findNumberOfLIS(vector<int> &nums)
{
if (nums.size() <= 1)
{
return nums.size();
}
vector<int> sortnums(nums);
sort(sortnums.begin(), sortnums.end());
Node nodes[nums.size() + 1] = {Node()};
Node ans = Node();
// 按nums[]顺序遍历,保证j<i这个条件,同时又用二分查找找出当前数num的下界nums[rank]
// 以nums[rank]结尾的LIS是最长的(之一),长度为lmax
// 长度为lmax的LIS个数已经在树状数组中,查询后可得到
// 把当前数num加到树状数组里面
for (auto num : nums)
{
// 二分搜索当前数的下界排名
int rank = lower_bound(sortnums.begin(), sortnums.end(), num) - sortnums.begin();
Node now = query(nodes, rank);
now.maxlength++;
now.cnt = max(now.cnt, 1);
ans += now;
add(nodes, rank + 1, now, nums.size());
}
return ans.cnt;
}
};
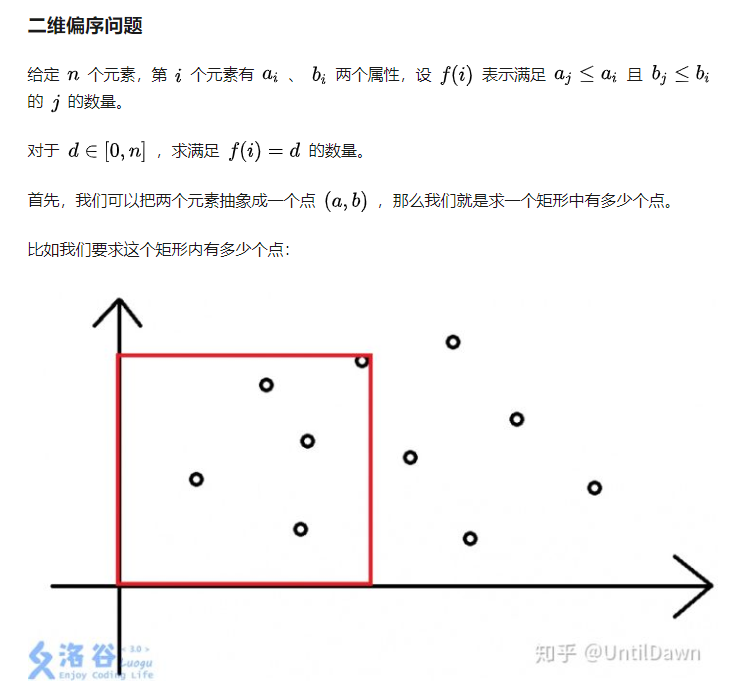
2. 什么是CDQ分治
LIS是一个二维偏序问题。
来看看LIS的状态转移方程:Lis[i]=max{Lis[j]+1} j<i && nums[j]<nums[i]
此处的点对是(i,nums[i])
cdq求LIS长度
cdq的本质:分治过程中用左边的信息更新右边的
状态定义
Length_Lis[i]表示以第i个元素为结尾的LIS长度
bool cmp(int a, int b)
{
if (nums_copy[a] == nums_copy[b])
return a > b;
return nums_copy[a] < nums_copy[b];
}
void cdq(int left, int right)
{
if (left == right)
{
if (!Length_Lis[left])
{
Length_Lis[left] = 1;
}
return;
}
int mid = (left + right) >> 1;
cdq(left, mid);
// 用左边的信息更新右边的
for (int i = left; i <= right; i++)
{
id[i] = i;
}
sort(id + left, id + right + 1, cmp);
int len = 0;
// 排序后的nums[left,right]单调递增
for (int i = left; i <= right; i++)
{
// 当前数在左边,左边已经有解,更新当前LIS长度
if (id[i] <= mid)
{
len = max(len, Length_Lis[id[i]]);
}
// 当前数在右边,更新LIS
// 满足二维偏序:id[i]<id[j] and nums[i]<nums[j]
else
{
Length_Lis[id[i]] = max(Length_Lis[id[i]], len + 1);
if (Length_Lis[id[i]] > Maxlen)
{
Maxlen = Length_Lis[id[i]];
}
}
}
cdq(mid+1,right);
}
那怎么求LIS个数呢?
定义状态
Num_Lis[i]表示以第i个元素为结尾的LIS的个数
在cdq递归结束后,再统计所有元素中的LIS的个数Maxnum
转移状态(用左边更新右边)的条件
首先一定要满足LIS的条件id[i]<id[j] and nums[i]<nums[j](二维偏序)
满足二维偏序后的两种转移方式:
- 以右边元素为结尾的LIS长度=以左边元素为结尾的LIS长度+1 –> 以右边元素为结尾的LIS个数+=以左边元素为结尾的LIS个数
- 以右边元素为结尾的LIS长度<以左边元素为结尾的LIS长度+1 –> 以右边元素为结尾的LIS个数=以左边元素为结尾的LIS个数;以右边元素为结尾的LIS长度=以左边元素为结尾的LIS长度+1
最长上升序列
特判一下以左边元素为结尾的LIS长度为0的情况,不转移
这一道题求的是最长上升序列的个数
最长上升序列!=最长不下降序列
[2,2,2,2,2]
LIS长度为1,个数为5
code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
int nums_copy[2005];
bool cmp(int a, int b)
{
if (nums_copy[a] == nums_copy[b])
return a > b;
return nums_copy[a] < nums_copy[b];
}
class Solution
{
public:
int Num_Lis[2005], id[2005], Length_Lis[2005];
int Maxnum = 0;
int Maxlen = 0;
void cdq(int left, int right)
{
if (left == right)
{
if (!Length_Lis[left])
{
Length_Lis[left] = 1;
Num_Lis[left] = 1;
}
return;
}
int mid = (left + right) >> 1;
cdq(left, mid);
// 用左边的信息更新右边的
for (int i = left; i <= right; i++)
{
id[i] = i;
}
sort(id + left, id + right + 1, cmp);
int len = 0;
int num = 0;
// 排序后的nums[left,right]单调递增
for (int i = left; i <= right; i++)
{
// 当前数在左边,左边已经有解,更新当前LIS长度
if (id[i] <= mid)
{
if (len < Length_Lis[id[i]])
{
len = Length_Lis[id[i]];
num = Num_Lis[id[i]];
}
else if (len == Length_Lis[id[i]])
{
num += Num_Lis[id[i]];
}
}
// 当前数在右边,更新LIS
// 满足二维偏序:id[i]<id[j] and nums[i]<nums[j]
else
{
// len=0表示没有信息可以转移
if (!len)
{
continue;
}
if (Length_Lis[id[i]] == len + 1)
{
Num_Lis[id[i]] += num;
}
else if (Length_Lis[id[i]] < len + 1)
{
Length_Lis[id[i]] = len + 1;
Num_Lis[id[i]] = num;
}
}
}
cdq(mid + 1, right);
}
int findNumberOfLIS(vector<int> &nums)
{
if (nums.size() <= 1)
return nums.size();
for (int i = 0; i < nums.size(); i++)
{
nums_copy[i] = nums[i];
}
cdq(0, nums.size() - 1);
Maxnum = 0;
Maxlen = 0;
for (int i = 0; i < nums.size(); i++)
{
if (Length_Lis[i] > Maxlen)
{
Maxlen = Length_Lis[i];
Maxnum = Num_Lis[i];
}
else if (Length_Lis[i] == Maxlen)
Maxnum += Num_Lis[i];
}
return Maxnum;
}
};
题后思考:为什么让相等的两个元素按原始位置倒序排列?
bool cmp(int a, int b)
{
// Why?
if (nums_copy[a] == nums_copy[b])
return a > b;
return nums_copy[a] < nums_copy[b];
}
如果正序会怎么样?
让我们对比两种排序方式产生的效果:
e.g.
1,2a,2b,4
(用a,b记录它们的原始位置)
1st:
if (nums_copy[a] == nums_copy[b])
return a > b;
1,2b,2a,4
2nd:
if (nums_copy[a] == nums_copy[b])
return a < b;
1,2a,2b,4
因为这道题求的是最长上升序列,所以2a的状态不能转移给2b。
按正序排列,2a的状态会转移给2b。
那如果我们特判在左边的前一个元素是否与当前右边的元素相等,也就是2a==2b?,这样是否可行呢?
if (pre == nums_copy[id[i]])
continue;
答案是不行,因为这样1的信息会丢失,无法转移到2b上。
写在最后
有一说一,cdq分治确实有点难度,我花了几天的时间在上面。
难点就在于怎么用左边的信息更新右边的,什么时候更新,而且不能用右边的信息更新右边的信息。
这种分治的思想确实很神奇。
当然,树状数组的解法也很神奇,这位大佬的题解值得一看。
最大子矩阵
二维前缀和
sum[i][j] =
sum[i][j - 1] + sum[i - 1][j] + matrix[i - 1][j - 1] - sum[i - 1][j - 1];
二维前缀和+暴力$O(n^2m^2)$
// O(n^2m^2)
if (n == 1 && m == 1)
return ans;
int sum[205][205];
// init
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] + matrix[i - 1][j - 1] - sum[i - 1][j - 1];
}
}
// brute force
int maxn = -(1 << 30);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
for (int k = i; k <= n; k++)
{
for (int w = j; w <= m; w++)
{
int curSum = sum[k][w] + sum[i - 1][j - 1] - sum[k][j - 1] - sum[i - 1][w];
if (curSum > maxn)
{
maxn = curSum;
ans[0] = i - 1, ans[1] = j - 1, ans[2] = k - 1, ans[3] = w - 1;
}
}
}
}
}
dp
一种错误的思路
事实证明,如果一开始思路是错的,怎么做都是错的
f[i][j]表示以(i,j)为右下角的最大矩阵和
f[i][j]=max{matrix[i][j],(i-1,j-1)转移,(i-1,j)转移,(i,j-1)转移}
g[i][j]表示以(i,j)为右下角的最大矩阵的左上角坐标
(i,j)从(i-1,j-1)或(i-1,j)或(i,j-1)转移过来:
x = g[i][j - 1].first, y = g[i][j - 1].second;
int left = sum[i][j] + sum[x][y] - sum[x][j] - sum[i][y];
x = g[i - 1][j].first, y = g[i - 1][j].second;
int top = sum[i][j] + sum[x][y] - sum[x][j] - sum[i][y];
x = g[i - 1][j - 1].first, y = g[i - 1][j - 1].second;
int diagonal = sum[i][j] + sum[x][y] - sum[x][j] - sum[i][y];
(看起来很有道理是吗?)
反例
-1 -2
8 -9
2 9
maxn=11!=10
2 9是转移不到的
注意:最优子结构和无后效性
正确的dp
把二维的最大矩阵和转化为一维的最大子段和
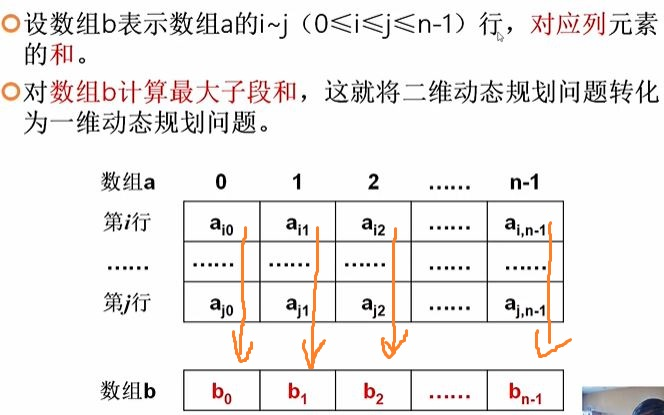
枚举i,j,求数组b的最大字段和
#include <vector>
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;
class Solution
{
public:
vector<int> getMaxMatrix(vector<vector<int>> &matrix)
{
int n = matrix.size();
int m = matrix[0].size();
vector<int> ans = {0, 0, 0, 0};
int row[205];
int maxn = -(1 << 30);
for (int i = 0; i < n; i++)
{
memset(row, 0, sizeof(row));
for (int j = i; j < n; j++)
{
int maxSum = 0;
int left = 0;
for (int k = 0; k < m; k++)
{
row[k] += matrix[j][k];
maxSum += row[k];
if (maxSum > maxn)
{
maxn = maxSum;
ans[0] = i, ans[1] = left, ans[2] = j, ans[3] = k;
}
if (maxSum < 0)
{
maxSum = 0;
left = k + 1;
}
}
}
}
return ans;
}
};
太难了,终于AC了
一道有趣的bfs题
分析
街道:把街道两侧的两个点(不包括街道所在的点)连接起来
如图所示,左上角的街道(0,0)将两个点(0,-1),(0,1)连接起来
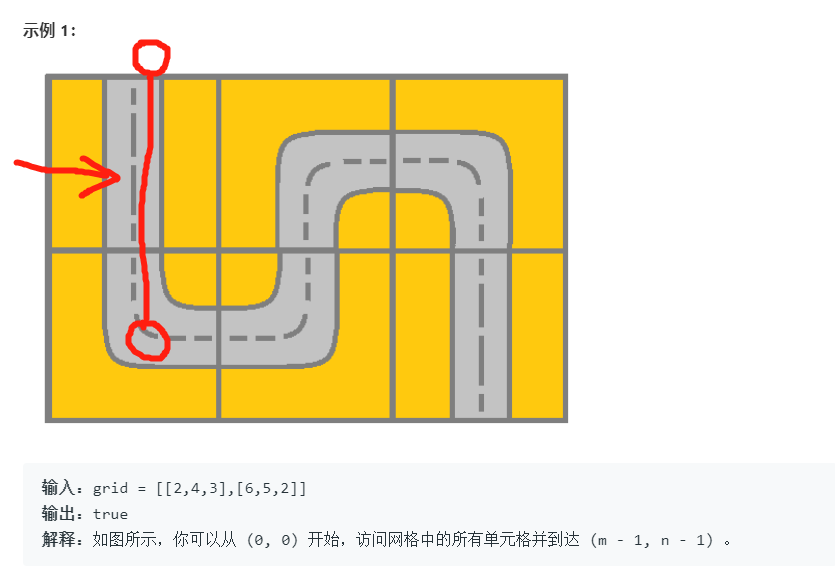
加到队列里面的是点,不是街道
定义完街道以后,可以开始遍历了,从左上角(0,0)开始bfs,看看当前点的街道把哪两个点连在一起了?
这里我加了两个数组简化程序,其中第0位是没用的,后面的第i位对应第i类街道
int xdir[7][2] = {{0, 0}, {1, -1}, {0, 0}, {-1, 0}, {1, 0}, {-1, 0}, {1, 0}};
int ydir[7][2] = {{0, 0}, {0, 0}, {-1, 1}, {0, 1}, {0, 1}, {0, -1}, {0, -1}};
等价于
switch (grid[y][x])
{
case 1:
q.push(make_pair(x + 1, y));
q.push(make_pair(x - 1, y));
break;
case 2:
q.push(make_pair(x, y - 1));
q.push(make_pair(x, y + 1));
break;
case 3:
q.push(make_pair(x - 1, y));
q.push(make_pair(x, y + 1));
break;
case 4:
q.push(make_pair(x + 1, y));
q.push(make_pair(x, y + 1));
break;
case 5:
q.push(make_pair(x - 1, y));
q.push(make_pair(x, y - 1));
break;
case 6:
q.push(make_pair(x + 1, y));
q.push(make_pair(x, y - 1));
}
但是光这样写不能AC,最后三个点过不去,为什么呢?
看一看数据:
[[1,1,2]]
横横竖
第二个点把第一和第三个点连起来了,但是第三个点是到不了第二个点的
所以我们不仅要判断从第一个点能否到第三个点,还要判断从第三个点能否回到第一个点
那就算一算呗:由当前点可以推出被当前点所在街道连接的两个点a,b,由a点所在的街道又可以推回来,看一看能否到达当前点,b点同理,也判断一次。
这样就能够保证该条街道是双向的了。
倒推回当前点的时候,要判断两个点,因为一条街道连接两个点,当前点可能是其中的一个
if (make_pair(x, y) == calNxt(grid, nx, ny, 0) || make_pair(x, y) == calNxt(grid, nx, ny, 1))
{
q.push(make_pair(nx, ny));
}
unordered_set
这个是用来查重的,就是一个存了pair的hash函数
重载hash函数那里我也不太懂,是抄别人的,可以上去看看官方文档
当找不到now的时候,mark.find(now)会返回mark.end()
找到now就说明这个点之前已经遍历过了,于是跳过它
if (mark.find(now) != mark.end())
continue;
code
448 ms 55.5 MB
双百(是因为交的人少)
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>
#include <unordered_set>
using namespace std;
class Solution
{
public:
int xdir[7][2] = {{0, 0}, {1, -1}, {0, 0}, {-1, 0}, {1, 0}, {-1, 0}, {1, 0}};
int ydir[7][2] = {{0, 0}, {0, 0}, {-1, 1}, {0, 1}, {0, 1}, {0, -1}, {0, -1}};
int n, m;
struct HashPair
{
size_t operator()(const pair<int, int> &key) const noexcept
{
return size_t(key.first) * 100000007 + key.second;
}
};
pair<int, int> calNxt(vector<vector<int>> &grid, int x, int y, int i)
{
int res = grid[y][x];
int nx = x + xdir[res][i], ny = y + ydir[res][i];
return make_pair(nx, ny);
}
bool hasValidPath(vector<vector<int>> &grid)
{
n = grid.size();
m = grid[0].size();
queue<pair<int, int>> q;
unordered_set<pair<int, int>, HashPair> mark;
q.push(make_pair(0, 0));
auto ans = make_pair(m - 1, n - 1);
while (!q.empty())
{
auto now = q.front();
q.pop();
if (now == ans)
{
return true;
}
int x = now.first, y = now.second;
// 这个点走过了
if (mark.find(now) != mark.end())
continue;
mark.insert(now);
for (int i = 0; i <= 1; i++)
{
auto [nx, ny] = calNxt(grid, x, y, i);
if (nx < 0 || nx >= m || ny < 0 || ny >= n)
{
continue;
}
if (make_pair(x, y) == calNxt(grid, nx, ny, 0) || make_pair(x, y) == calNxt(grid, nx, ny, 1))
{
q.push(make_pair(nx, ny));
}
}
}
return false;
}
};
并查集?
根据分析,一条街道就是把两个点连接起来,问题就是求(0,0)和(m-1,n-1)是否连通
这不就可以用并查集了吗?
如果当前点所在的街道是双向的,就合并该街道两端的点。
最后查询(0,0)和(m-1,n-1)的祖先是否相等
相等就说明两个点连通
code
264 ms 24.2 MB
这个更快,更省空间哦
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int xdir[7][2] = {{0, 0}, {1, -1}, {0, 0}, {-1, 0}, {1, 0}, {-1, 0}, {1, 0}};
int ydir[7][2] = {{0, 0}, {0, 0}, {-1, 1}, {0, 1}, {0, 1}, {0, -1}, {0, -1}};
int f[90005];
pair<int, int> calNxt(vector<vector<int>> &grid, int x, int y, int i)
{
int res = grid[y][x];
int nx = x + xdir[res][i], ny = y + ydir[res][i];
return make_pair(nx, ny);
}
int find(int x)
{
if (x == f[x])
return x;
f[x] = find(f[x]);
return f[x];
}
void merge(int x, int y)
{
int fx = find(x), fy = find(y);
if (fx != fy)
{
f[fx] = fy;
}
}
bool hasValidPath(vector<vector<int>> &grid)
{
int n = grid.size();
int m = grid[0].size();
for (int i = 1; i <= n * m; i++)
{
f[i] = i;
}
for (int y = 0; y < n; y++)
{
for (int x = 0; x < m; x++)
{
for (int i = 0; i <= 1; i++)
{
auto [nx, ny] = calNxt(grid, x, y, i);
if (nx < 0 || nx >= m || ny < 0 || ny >= n)
{
continue;
}
if (make_pair(x, y) == calNxt(grid, nx, ny, 0) || make_pair(x, y) == calNxt(grid, nx, ny, 1))
{
merge(x + y * m, nx + ny * m);
}
}
}
}
int st = 0, end = (n - 1) * m + m - 1;
if (find(st) == find(end))
return true;
return false;
}
};
题后总结
其实这道题我比赛的时候也没有做出来,过一会再做就想出来了,看来还是比赛经验不足,紧张了
Google Kick Start
2020 Round A
Plate: 背包
Dr. Patel has N stacks of plates. Each stack contains K plates.
Each plate has a positive beauty value, describing how beautiful it looks.
Dr. Patel would like to take exactly P plates to use for dinner tonight.
If he would like to take a plate in a stack, he must also take all of the plates above it in that stack as well.
Help Dr. Patel pick the P plates that would maximize the total sum of beauty values.
这其实是一道变形的分组背包,十分简单,但是我做了一个多小时…
分析
有N个栈,想要取出某个栈中的盘子,就一定要把在它前面的都取出来
转化一下问题:有N类物品,每一类最多取一个物品,求体积为P的背包能容纳的最大物品价值.
一个栈就是一类物品,里面每个物品的价值为盘子的前缀和,重量为它加上它前面的盘子数量.

code
f[v] = max(f[v], f[v - j] + sum[i][j])
这里的j就是物品重量,sum[i][j]就是物品价值
#include <algorithm>
#include <queue>
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
int f[1505];
int sum[51][31];
int main()
{
int T;
cin >> T;
for (int caseNum = 1; caseNum <= T; caseNum++)
{
int n, k, plateNum;
cin >> n >> k >> plateNum;
printf("Case #%d: ", caseNum);
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; i++)
{
int res;
sum[i][0] = 0;
for (int j = 1; j <= k; j++)
{
scanf("%d", &res);
sum[i][j] = sum[i][j - 1] + res;
}
}
for (int i = 1; i <= n; i++)
{
for (int v = plateNum; v >= 0; v--)
{
for (int j = 1; j <= min(k, v); j++)
{
f[v] = max(f[v], f[v - j] + sum[i][j]);
}
}
}
int ans = f[plateNum];
printf("%d\n", ans);
}
return 0;
}
Workout
Problem:
Tambourine has prepared a fitness program so that she can become more fit! The program is made of N sessions. During the i-th session, Tambourine will exercise for Mi minutes. The number of minutes she exercises in each session are strictly increasing.
The difficulty of her fitness program is equal to the maximum difference in the number of minutes between any two consecutive training sessions.
To make her program less difficult, Tambourine has decided to add up to K additional training sessions to her fitness program. She can add these sessions anywhere in her fitness program, and exercise any positive integer number of minutes in each of them. After the additional training session are added, the number of minutes she exercises in each session must still be strictly increasing. What is the minimum difficulty possible?
错误的思路
差分后每次取差分数组的最大值,把最大值/2再插入到差分数组中
反例:
[2, 12] → [2, 7, 12] difficulty=5 → [2, 7, 9, 12] difficulty=5
[2, 12] → [2, 5, 12] difficulty=7 → [2, 5, 8, 12] difficulty=4
程序结果:
difficulty=10 -> 5 -> 3
这是无法做到的
正解
- 确定最终
difficulty的值 - 验证能否满足最多插入
K个数的条件
设当前的difficulty=d
每个区间能插入的数的个数为ceil(区间长度/d)-1
遍历每个区间,算出要插入的数的个数的总和kSum
找出第一个使kSum<=K的d即为答案
注意到d越大,kSum越小,所以能用二分搜索找到使kSum<=K的d的最小值
要把d[i]变成float
否则ceil(1/3)=ceil(0)=0
ceil(d[i] * 1.0 / mid) - 1
#include <iostream>
#include <cmath>
using namespace std;
int a[100005];
int d[100005];
void solve()
{
int n, k;
cin >> n >> k;
a[0] = 0;
int maxn = 0;
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
d[i] = a[i] - a[i - 1];
maxn = max(maxn, d[i]);
}
int left = 1, right = maxn;
while (left < right)
{
int mid = (left + right) >> 1;
int kSum = 0;
for (int i = 2; i <= n && kSum <= k; i++)
{
kSum += ceil(d[i] * 1.0 / mid) - 1;
}
if (kSum > k)
{
left = mid + 1;
}
else
{
right = mid;
}
}
printf("%d\n", left);
}
int main()
{
int T;
cin >> T;
for (int caseNum = 1; caseNum <= T; caseNum++)
{
printf("Case #%d: ", caseNum);
solve();
}
return 0;
}
3.15 Notes
3.9-3.15 Learning Notes
Leetcode Algorithm
不使用额外空间
不用额外空间意味着只能在原地操作,而在原地操作需要注意不能影响到还未计算的部分。
基本思路:把已经计算过的部分视为新数组,在这部分里面操作不会影响到后面的结果。
特殊的优先队列
这题不能直接套优先队列(堆)模板,因为这里面的pop_front是要返回原队列的头部,不是优先队列的头部(max/min)。但是max_value又需要在O(1)内完成查询,所以只用一个队列肯定不行。
于是我们需要用到一个神奇的辅助队列sort_queue,它的头部就是max_value。
- 如何维护
sort_queue? - 原始队列发生
pop_front时sort_queue该怎么变动?
完全背包的变体:求最小物品数
只会做背包类dp的我笑了
延伸阅读:背包九讲
二叉树的直径
计算二叉树的直径长度
一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
遍历每一个节点计算它的深度及经过它的最大直径长度
直径长度=左孩子深度+右孩子深度-根节点深度*2depth[lchild]+depth[rchild]-depth[node]*2]
二叉树中的最大路径和
是上一题的进阶版
跟上一题不一样,路径长度可能负值,所以遍历每个节点的时候不能直接算以当前节点为根节点的子树的所有路径长度之和。
如果左子树或右子树路径长度之和小于零就要舍去。
最长路径有三种情况:
a.father
\
a
/ \
b c
- b->a->c
- a.father->a->b
- a.father->a->c
递归的时候怎么写呢?
def dfs(root: TreeNode) -> int:
nonlocal max_path_sum
if root is None:
return 0
left_val = max(0, dfs(root.left))
right_val = max(0, dfs(root.right))
node_val = max(left_val, right_val)+root.val
max_path_sum = max(max_path_sum, left_val+right_val+root.val)
return node_val
为什么只用max_path_sum = max(max_path_sum, left_val+right_val+root.val)就可以取三种情况中的最大值?
注意到return node_val = max(left_val, right_val)+root.val,以上面为例子,dfs(a.father)=max(a.father->a->b,a.father->a->c)实际上在上一层递归中已经计算了三种情况中的后两种,所以只需要计算第一种即可。
一个写递归的小心得
不要用脑子套进去一层层计算,要相信dfs(a)返回的就是a的node_val,不需要管里面的一层套一层的逻辑,只需要写好其中一层的逻辑,它自然就能够跑起来
gcd in string
求两个字符串的最大公因子
十分有趣的一道题,求两个数的最大公因子自然用欧几里得算法
def gcd(a,b):
if a<b:
a,b=b,a
if b==0:
return a
gcd(b,a%b)
那求两个字符串该怎么办呢?
一个很棒的题解
判断是否有解
str1+str2=str2+str1有解的话最大公因子的长度是不是两个字符串长度的gcd?
是的,因为如果能循环以它的约数为长度的字符串,自然也能够循环以它为长度的字符串,所以这个理论长度就是我们要找的最优解。
求众数
pairing阶段:两个不同选票的人进行对抗,并会同时击倒对方,当剩下的人都是同一阵营,相同选票时,结束。
counting阶段:计数阶段,对最后剩下的下进行选票计算统计,判断选票是否超过总票数的一半,选票是否有效。
出现次数大于n/2
这题有很多种做法:
- 排序后中间元素即为众数
- hashtable存储
- 随机选取并验证
- 分治
- 摩尔投票法
出现次数大于n/3
上一题是选一个代表,这题是选两个代表
本质是选票抵消,但是需要注意代码逻辑
买卖股票的最佳时机*6
(但是我还是不会怎么买卖股票)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
I
如果你最多只允许完成一笔交易(即买入和卖出一支股票)max(price[i]-price[j]) (i>j)
II
你可以尽可能地完成更多的交易(多次买卖一支股票)
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
贪心:当前策略总是全局最佳策略
今天比昨天高就买,否则不买
III
你最多可以完成两笔交易
方法一
遍历划分点,把数组分成两部分,分别计算两部分的最大利润,相当于第一题
但是直接算会超时,这里用一个小优化,提前算好从左边到划分点的最大利润left_max和从有右边到划分点的最大利润right_max
算right_max时注意要逆向思考,记录的是max_price
code
class Solution:
def maxProfit(self, prices) -> int:
if not prices:
return 0
# left_max: [0,i] max profit
left_max = [0] * len(prices)
min_price = prices[0]
for i in range(1, len(prices)):
min_price = min(min_price, prices[i])
left_max[i] = max(left_max[i - 1], prices[i] - min_price)
# right_max: [i,len-1] max profit
right_max = [0] * len(prices)
max_price = prices[-1]
for i in range(len(prices)-2, -1, -1):
max_price = max(max_price, prices[i])
right_max[i] = max(right_max[i + 1], max_price-prices[i])
max_profit = 0
for i in range(0, len(prices)):
max_profit = max(max_profit, left_max[i]+right_max[i])
return max_profit
方法二
状态定义
f[i][j][k]表示第i天,进行了j次交易,当前状态为k时的最大利润
该题中$j<=2$
k=0表示没有持有股票,k=1表示持有股票
状态转移方程
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0])
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1])
初始状态定义
f[i][0][0] = 0
f[i][0][1] = -inf
f[0][i][0] = -inf
f[0][i][1] = -inf
code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxProfit(vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
int f[30000 + 5][3][2];
for (int i = 0; i <= n; i++)
{
f[i][0][0] = 0;
f[i][0][1] = -inf;
}
for (int i = 1; i <= 2; i++)
{
f[0][i][0] = -inf;
f[0][i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= 2; j++)
{
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0]);
if (j)
{
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1]);
}
}
}
return max(max(f[n][0][0], f[n][1][0]), f[n][2][0]);
}
};
IV
你最多可以完成 k 笔交易
这道题就用通解
注意当k>=n的时候转化为第二题的情况,直接用贪心算法。不然时间和空间都会爆炸的。
code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxProfit(int k, vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
// 用贪心处理能随意买卖的情况
if (k >= n)
{
int profit = 0;
for (int i = 1; i < n; i++)
{
if (prices[i] > prices[i - 1])
{
profit += prices[i] - prices[i - 1];
}
}
return profit;
}
int f[n + 5][k + 1][2];
for (int i = 0; i <= n; i++)
{
f[i][0][0] = 0;
f[i][0][1] = -inf;
}
for (int i = 1; i <= k; i++)
{
f[0][i][0] = -inf;
f[0][i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= k; j++)
{
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0]);
if (j)
{
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1]);
}
}
}
int maxProfit = 0;
for (int i = 0; i <= k; i++)
maxProfit = max(maxProfit, f[n][i][0]);
return maxProfit;
}
};
with cooldown
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
无限制交易次数
状态转移方程要改一改
原来的:
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0])
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1])
现在要把第二维状态压掉并改一下卖股票的那条方程,相当于要过两天才能收到卖股票的钱
f[i][0] = max(f[i - 2][1] + prices[i - 2], f[i - 1][0]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]);
还要判断一下边界,因为如果最后一天卖出的话,就会收不到钱
f[n + 1][0] = max(f[n - 1][1] + prices[n - 1], f[n][0]);
return max(f[n + 1][0], f[n][0]);
code
class Solution
{
public:
int maxProfit(vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
if (!n){
return 0;
}
int f[n + 5][2];
for (int i = 0; i <= n + 1; i++)
{
f[i][0] = 0;
f[i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
if (i >= 2)
{
f[i][0] = max(f[i - 2][1] + prices[i - 2], f[i - 1][0]);
}
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]);
}
f[n + 1][0] = max(f[n - 1][1] + prices[n - 1], f[n][0]);
return max(f[n + 1][0], f[n][0]);
}
};
一种更快的方法
把冷冻期也视为一种状态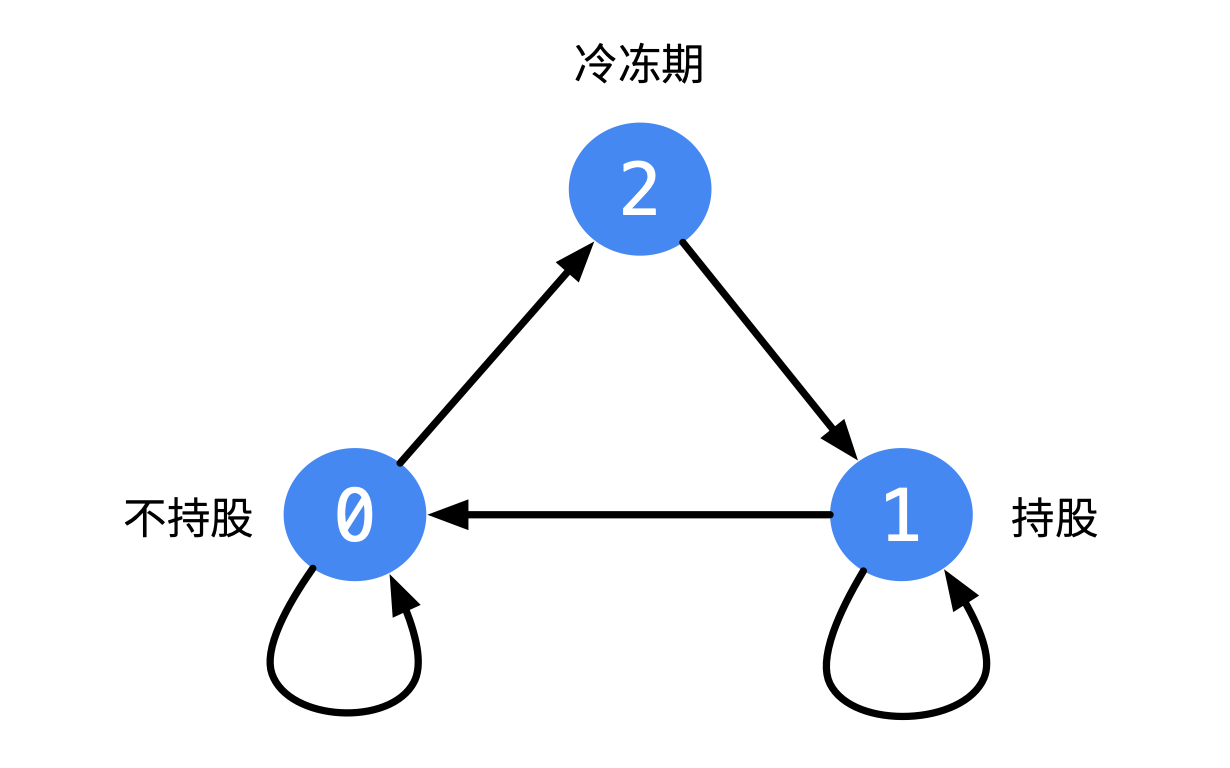
再加上滚动变量
code
int f[3];
f[0] = 0;
f[1] = -inf;
f[2] = 0;
int preCash = f[0];
int preStock = f[1];
for (int i = 1; i <= n; i++)
{
f[0] = max(preCash, preStock + prices[i - 1]);
f[1] = max(preStock, f[2] - prices[i - 1]);
f[2] = preCash;
preCash = f[0];
preStock = f[1];
}
return max(f[0], f[2]);
with transaction fee
你可以无限次地完成交易,但是你每次交易都需要付手续费。
改一点点就可以了,买的时候把fee减掉
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]-fee);
code
压缩状态,当前状态只依赖于上一状态
class Solution
{
public:
int maxProfit(vector<int> &prices, int fee)
{
const int inf = 1 << 30;
const int n = prices.size();
if (n <= 1)
{
return 0;
}
int f[2][2];
f[0][0] = 0;
f[0][1] = -inf;
for (int i = 1; i <= n; i++)
{
f[i&1][0] = max(f[i - 1&1][1] + prices[i - 1], f[i - 1&1][0]);
f[i&1][1] = max(f[i - 1&1][1], f[i - 1&1][0] - prices[i - 1] - fee);
}
return f[n&1][0];
}
};
Eight Queens
求解决方案
dfs+回溯
从第一行开始放,一直放到最后一行
用四个bool数组判断行,列,左对角线,右对角线有没有皇后
dfs出来记得把状态恢复原位
只要一个方案
找到一个直接exit()
求方案个数
进阶:状态压缩+位运算
先上代码
code
#include <iostream>
using namespace std;
class Solution
{
public:
int ans = 0;
int full;
void dfs(int col, int leftdown, int rightdown)
{
if (col == full) //每一列都已经有皇后了,说明满了
{
++ans;
return;
}
// col|leftdown|rightdown 任何一个是1都不行,表示在皇后攻击范围内
// 取反后,1是可以放的位置,0是不能放的
// 与 11111(n个1)与运算后把高位舍去,剩下的位数为棋盘的边长
int now = full & ~(col | leftdown | rightdown);
while (now)
{
// 取最低一位1,表示在这里放一个皇后
int lowbit = now & -now;
now -= lowbit;
// 更新3个状态
// row是没有用的,因为row已经包含在col里面了
// col=col+lowbit
// leftdown=(leftdown+lowbit)<<1
// rightdown=(rightdown+lowbit)>>1
dfs(col + lowbit, (leftdown + lowbit) << 1, (rightdown + lowbit) >> 1);
}
}
int totalNQueens(int n)
{
full = (1 << n) - 1;
dfs(0, 0, 0);
return ans;
}
};
一种非常牛逼的解法,需要有高超的位运算能力。
简单来说,就是把原来的4个bool数组压缩成了3个int数,用这三个数的每一位表示约束条件。
因为不需要输入方案,只求方案个数,所以不需要存储之前的皇后位置。
状态表示
1表示在皇后的攻击范围里面0表示可以放皇后
full
n=5
full=2^5-1=31=11111
5个1表示放满了
lowbit
取二进制数的最低位
在while里面起到遍历当前行所有能放皇后的位置
lowbit(x)=x&-x
col
这个最容易理解,如果某一位上是1,就说明之前在这列上有皇后。
位数对应列数
假设现在dfs到第三行,前面两行的皇后分别放在第一和第四列
1 0 0 0
0 0 0 1
1 0 0 1
col=1001
leftdown
右上到左下的对角线,加上当前行的皇后位置后,整体左移一位
dfs到第三行
0 0 1 0
1 0 0 0
1 1 0 0 0
leftdown=11000
实际上最高位的1被舍去了,因为有full&
rightdown
左上到右下的对角线,加上当前行的皇后位置后,整体右移一位
0 1 0 0
0 0 0 1
0 0 0 1 1
rightdown=00011
实际上最右侧的1被舍去了,位运算的overflow
求所有方案
算法核心是一样的,只不过需要在每一步记录下皇后的位置。
class Solution {
public:
vector<vector<string>> ans;
vector<string> cur;
int full;
void dfs(int col, int leftdown, int rightdown,int n)
{
if (col == full) //每一列都已经有皇后了,说明满了
{
ans.push_back(cur);
return;
}
// col|leftdown|rightdown 任何一个是1都不行,表示在皇后攻击范围内
// 取反后,1是可以放的位置,0是不能放的
// 与 11111(n个1)与运算后把高位舍去,剩下的位数为棋盘的边长
int now = full & ~(col | leftdown | rightdown);
while (now)
{
// 取最低一位1,表示在这里放一个皇后
int lowbit = now & -now;
now -= lowbit;
// 更新3个状态
// row是没有用的,因为row已经包含在col里面了
// col=col+lowbit
// leftdown=(leftdown+lowbit)<<1
// rightdown=(rightdown+lowbit)>>1
string s;
int tmp=lowbit;
while (tmp)
{
if (tmp&1)
s.push_back('Q');
else
s.push_back('.');
tmp=tmp>>1;
}
while (s.size()<n)
s.push_back('.');
reverse(s.begin(),s.end());
cur.push_back(s);
dfs(col + lowbit, (leftdown + lowbit) << 1, (rightdown + lowbit) >> 1,n);
cur.pop_back();
}
}
vector<vector<string>> solveNQueens(int n) {
ans.clear();
cur.clear();
full = (1 << n) - 1;
dfs(0, 0, 0,n);
return ans;
}
};
Dancing Link 听说更快哦
夜深人静写算法(九)- Dancing Links X(跳舞链)
LIS
O(n^2) dp
Lis[i]表示以nums[i]为结尾的最长上升序列的长度
Lis[i]=max(Lis[j]+1) j<i and nums[j]<nums[i]
O(nlogn) 二分+贪心
Lis[]存储当前的最长上升序列
如果当前的数比Lis中最后一位还要大,Lis[++ans]=nums[i]
如果小的话,就在Lis数组(单调递增)中二分查找大于等于nums[i]的第一个数
code
class Solution
{
public:
int lengthOfLIS(vector<int> &nums)
{
int Lis[10005];
if (nums.size() <= 1)
{
return nums.size();
}
Lis[1] = nums[0];
int ans = 1;
for (int i = 1; i < nums.size(); i++)
{
if (nums[i] > Lis[ans])
{
Lis[++ans] = nums[i];
continue;
}
int left = 1, right = ans;
while (left < right)
{
int mid = (left + right) >> 1;
if (Lis[mid] >= nums[i])
{
right = mid;
}
else
{
left = mid + 1;
}
}
Lis[left] = nums[i];
}
return ans;
}
};
变式:求LIS的数量
说实话,这题想了挺久的,也调了很久。
dp
与求LIS的O(n^2)算法类似,多维护一个MaxLength[]数组,记录到当前位置LIS的长度
j<i && nums[j]<nums[i]
// Lis[i] == Lis[j] + 1 说明之前已经找到长度为Lis[i]的LIS了 现在还有一种方案,于是将两种方案数相加
if (Lis[i] == Lis[j] + 1)
{
MaxLength[i] += MaxLength[j];
}
// Lis[i] < Lis[j] + 1 说明之前没有找到LIS,直接将方案数转移
else if (Lis[i] < Lis[j] + 1)
{
Lis[i] = Lis[j] + 1;
MaxLength[i] = MaxLength[j];
}
code
class Solution
{
public:
int findNumberOfLIS(vector<int> &nums)
{
int Lis[10005];
int MaxLength[10005];
if (nums.size() <= 1)
{
return nums.size();
}
int LisLength = 1;
int ans = 0;
for (int i = 0; i < nums.size(); i++)
{
MaxLength[i] = 1;
Lis[i] = 1;
}
for (int i = 0; i < nums.size(); i++)
{
for (int j = 0; j < i; j++)
{
if (nums[i] <= nums[j])
{
continue;
}
if (Lis[i] == Lis[j] + 1)
{
MaxLength[i] += MaxLength[j];
}
else if (Lis[i] < Lis[j] + 1)
{
Lis[i] = Lis[j] + 1;
MaxLength[i] = MaxLength[j];
}
}
// 一边遍历一遍维护答案
if (Lis[i] > LisLength)
{
LisLength = Lis[i];
ans = MaxLength[i];
}
else if (Lis[i] == LisLength)
{
ans += MaxLength[i];
}
}
return ans;
}
};
线段树
岛屿
dfs
小优化:不需要用额外的bool数组记录是否访问过,直接将访问过的陆地变为水就可以了。
注意area的计算,每次dfs到下一个点,都要更新area的值并返回给上一个点,这样就能保证dfs入口处返回的area是总的大小
code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxArea = 0;
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int dfs(vector<vector<int>> &grid, int row, int col, int area)
{
grid[row][col] = 0;
for (int i = 0; i < 4; i++)
{
int nxtRow = row + dir[i][0];
int nxtCol = col + dir[i][1];
if (nxtRow < 0 || nxtRow >= grid.size() || nxtCol < 0 || nxtCol >= grid[0].size())
continue;
if (grid[nxtRow][nxtCol])
{
area = dfs(grid, nxtRow, nxtCol, area + 1);
}
}
return area;
}
int maxAreaOfIsland(vector<vector<int>> &grid)
{
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[i].size(); j++)
{
if (grid[i][j])
{
maxArea = max(dfs(grid, i, j, 1), maxArea);
}
}
}
return maxArea;
}
};
变式:求岛屿数量
比上一题简单一点,只需要记录dfs了多少次即可,不需要求面积。
int maxAreaOfIsland(vector<vector<int>> &grid)
{
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[i].size(); j++)
{
if (grid[i][j])
{
maxArea = max(dfs(grid, i, j, 1), maxArea);
}
}
}
return maxArea;
}
3.8 Notes
3.2-3.8 Learning Notes
CSAPP
int compare with unsigned int
If there is a mix of unsigned and signed in single expression,
signed values implicitly cast to unsigned
2’s Complement–>补码
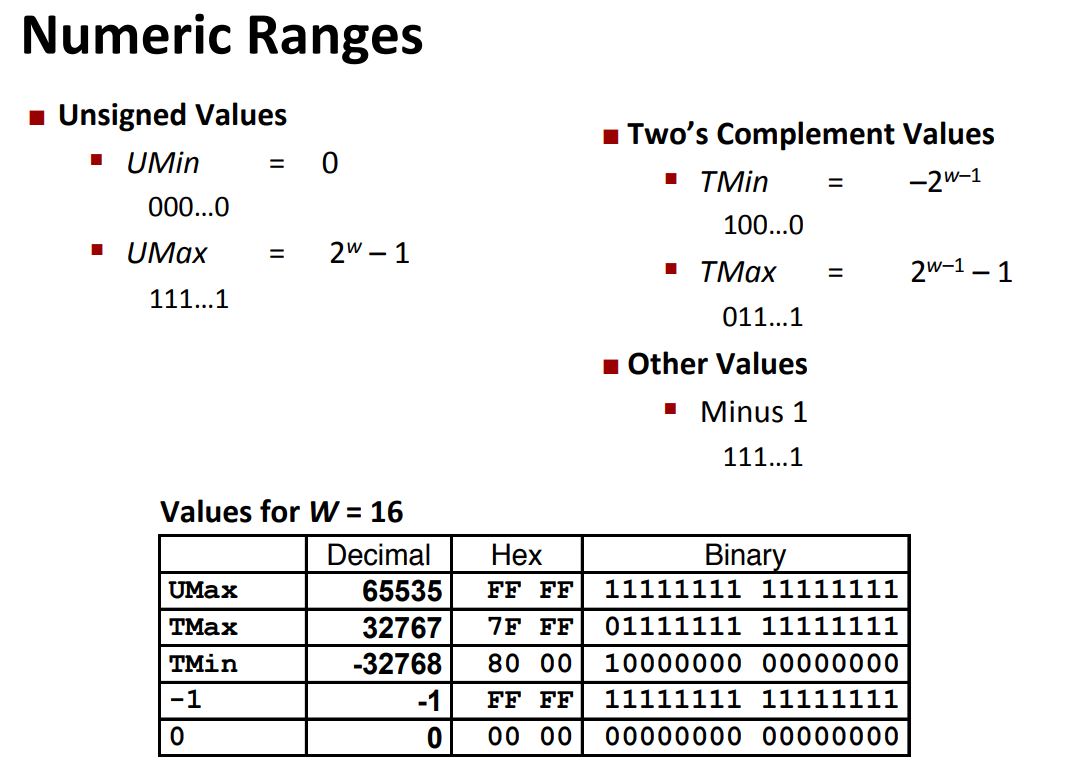
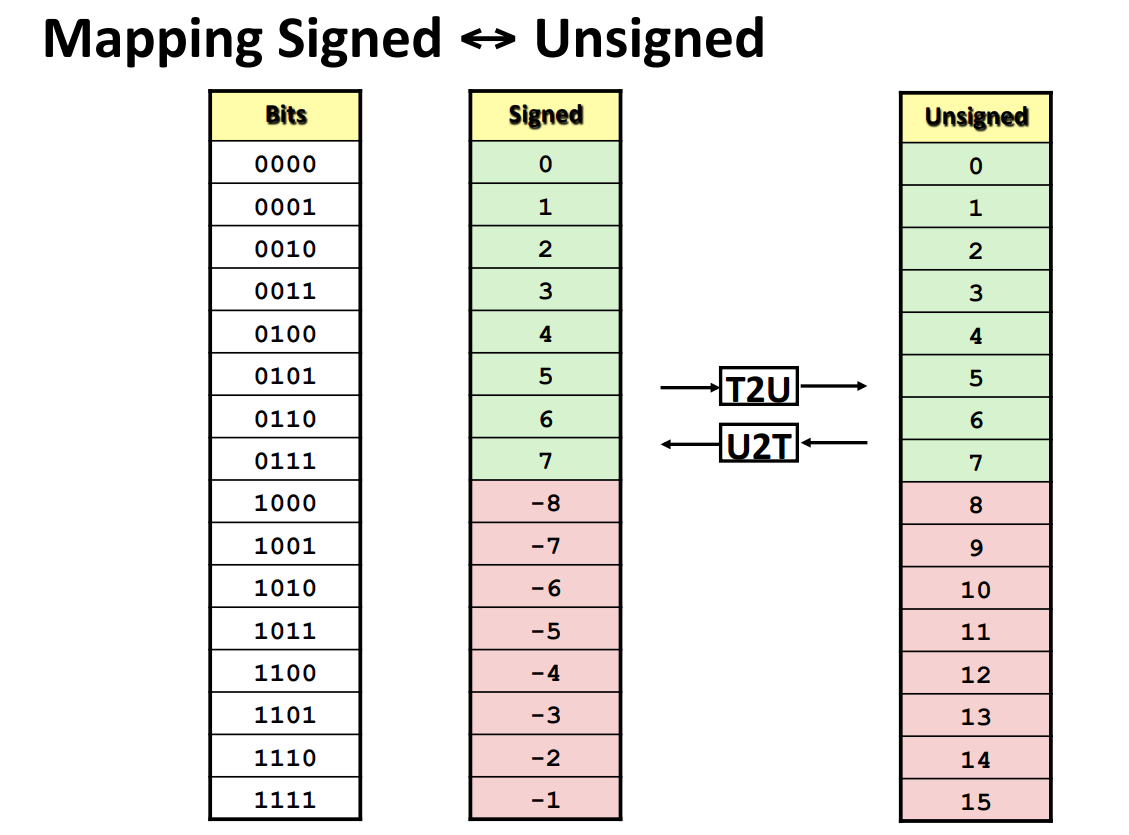
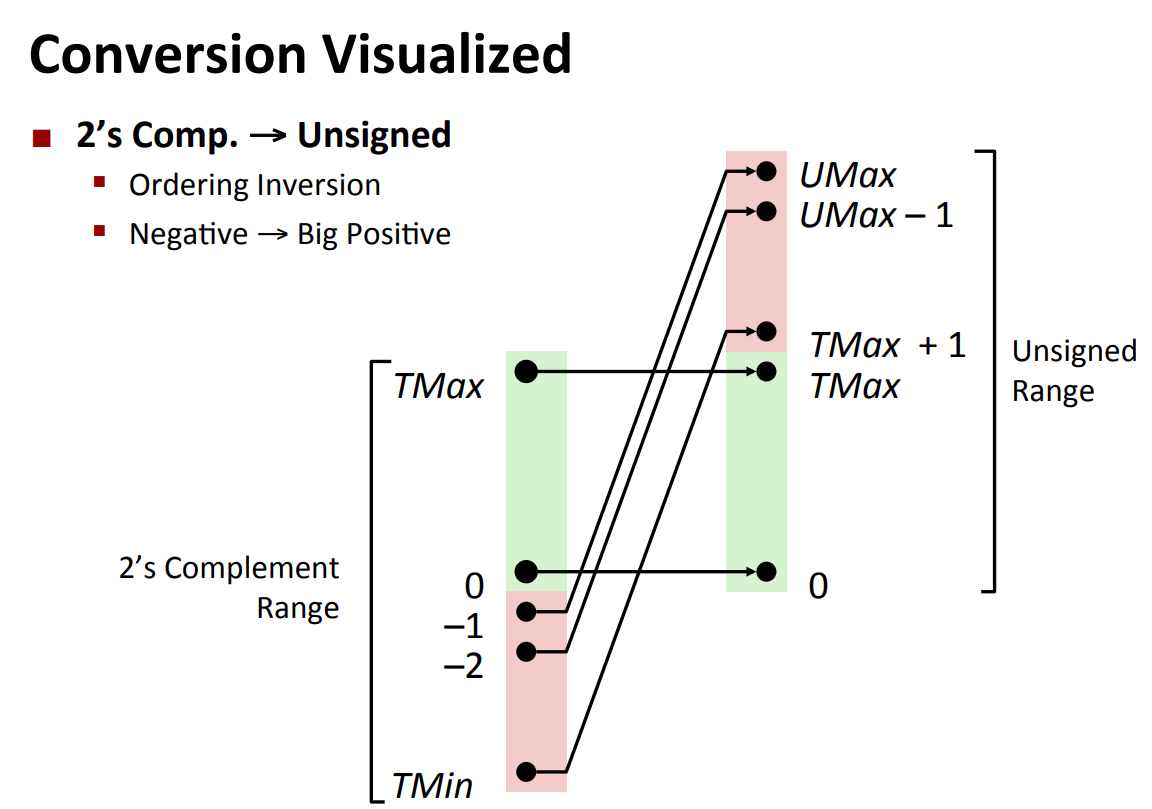
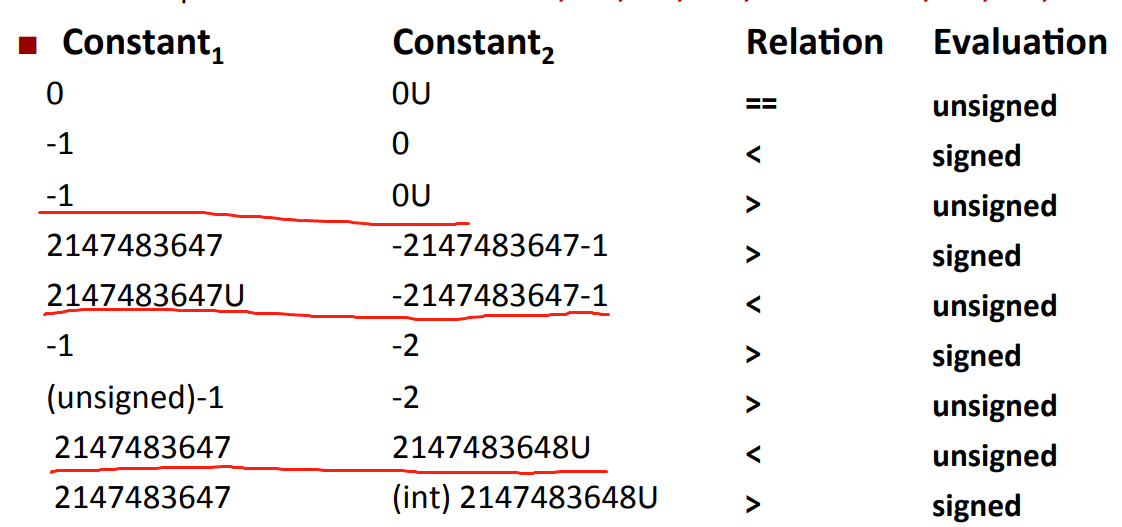
Expanding
- Unsigned: add zeros
- Signed: sign extension:convert w-bit signed int x to w+k-bit int with same value

Overflow
Add
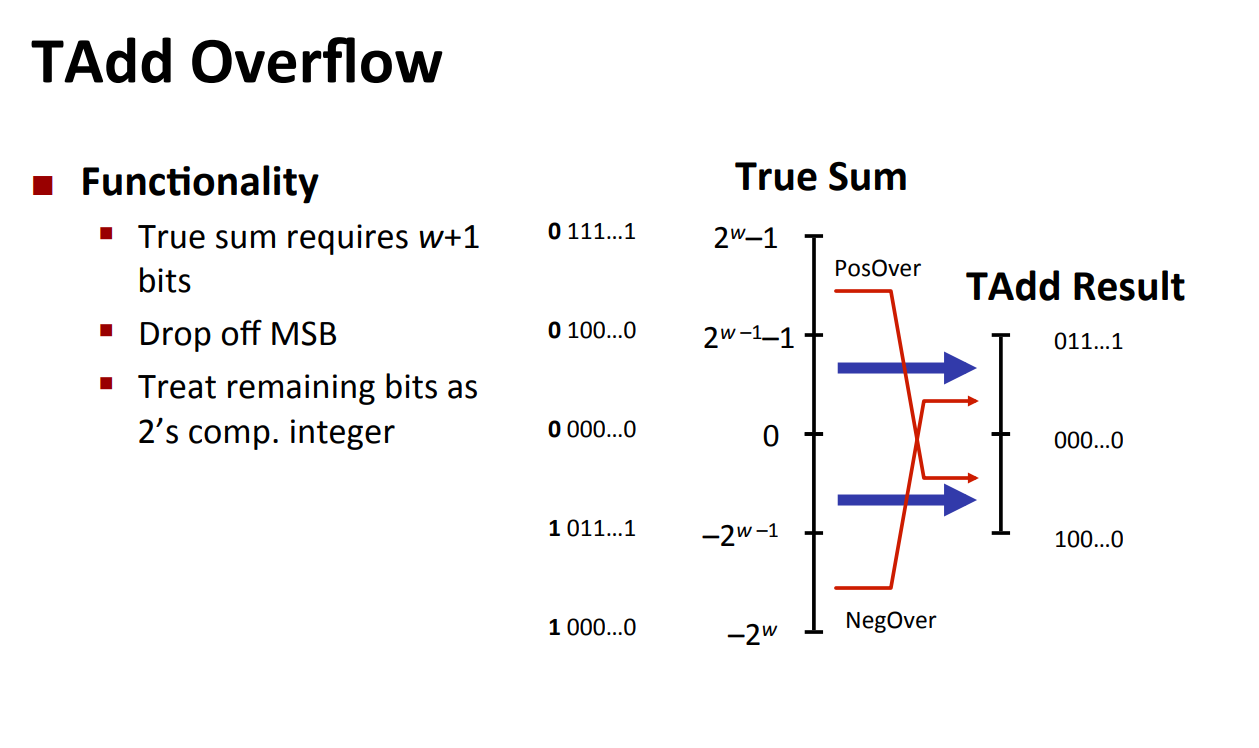
Multiplication
Use shift to replace multiply because it’s much faster
u<<3==u*8
(u<<5)-(u<<3)==u*24
How to use the unsigned

i will go around and become larger than cnt.
It works even if cnt is signed and <0
Integer Puzzles

- overflow in + and *
- TMin (TMin取反后还是自己,因为只有它不对称)
- transformation between signed and unsigned
Shift

- logical shift: Fill with 0 on left
- arithmetic shift: Replicate most significant bit on left
Division for signed number
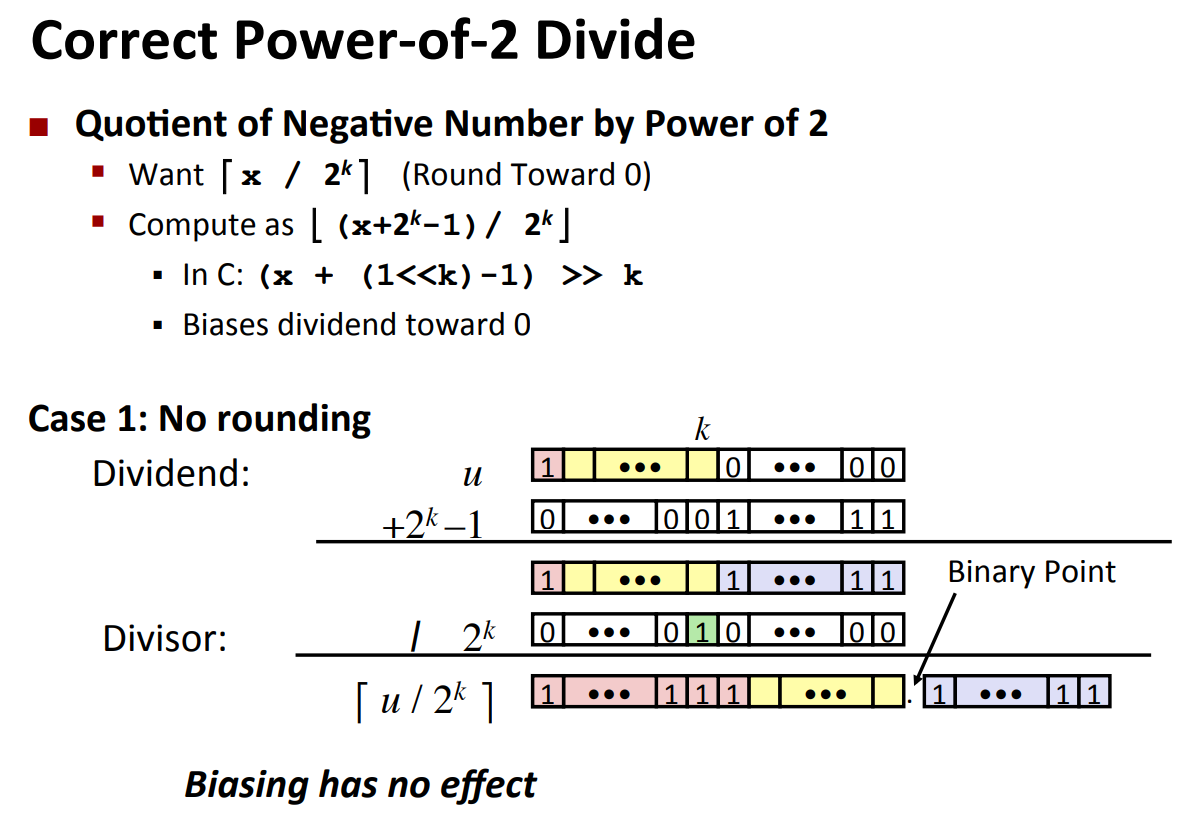
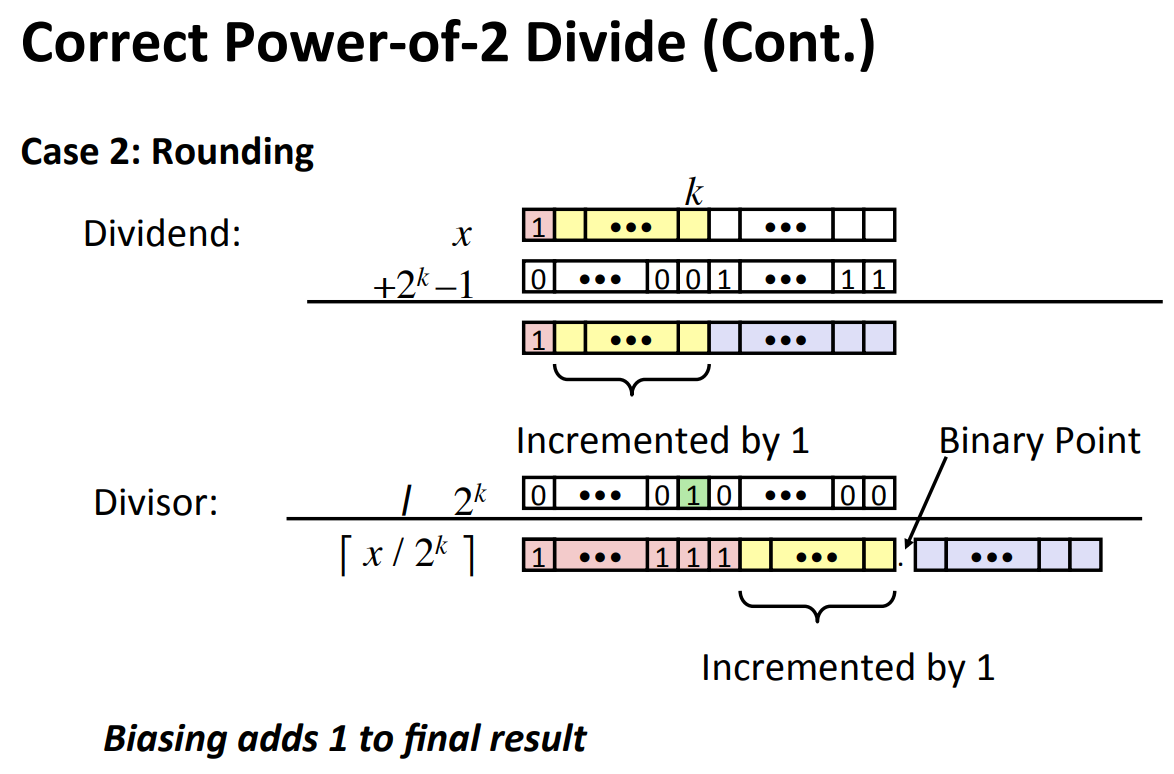
红色是符号位和arithmetic shift
黄色是数字位
+2^k-1可能会让数字位+1,这样商也会+1